- Die
Heaviside-Funktion
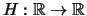 hat eine Sprungstelle
bei 0, da
hat eine Sprungstelle
bei 0, da
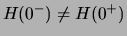 .
.
- Im Falle monotoner Funktionen
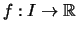 besteht die Menge
der Unstetigkeitsstellen
nur aus Sprungstellen.
besteht die Menge
der Unstetigkeitsstellen
nur aus Sprungstellen.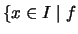 ist unstetig in
ist unstetig in 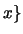
- Für die Gauß-Klammer-Funktion
![$ G:x\mapsto [x]$](img1375.png) ist die Menge der Unstetigkeitsstellen gleich
ist die Menge der Unstetigkeitsstellen gleich
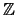 .
.
- Auf
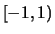 definieren wir eine Funktion
und setzen sie zu einer auf ganz
definieren wir eine Funktion
und setzen sie zu einer auf ganz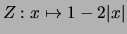
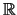 definierten
definierten 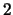 -periodischen
Zackenfunktion fort:
-periodischen
Zackenfunktion fort:
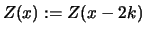 für
für
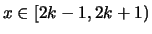 ,
,
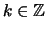 ,
,
D. h. es gilt
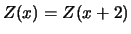 für alle
für alle
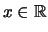 .
Da
.
Da
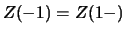 gilt, ist
gilt, ist 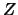 auf
auf
 stetig.
stetig.
Da
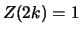 und
und
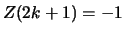 für alle
für alle
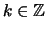 gilt, existieren
die Grenzwerte von
gilt, existieren
die Grenzwerte von
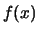 für
für
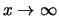 und
und
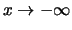 nicht.
nicht.
Später werden wir statt der Zackenfunktion die
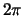 -periodische Funktion
-periodische Funktion 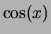 betrachten.
betrachten.
- Mit der Zackenfunktion
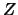 können wir die
Wackelfunktion
können wir die
Wackelfunktion
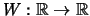 bilden:
bilden:
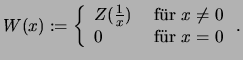
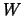 ist stetig auf
ist stetig auf
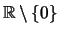 .
.
Die Wackelfunktion oszilliert links und rechts von 0.
Die Grenzwerte von
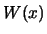 für
für
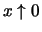 und
und
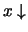 existieren nicht.
existieren nicht.
Auch durch Abänderung von
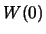 kann
kann  nicht zu einer in 0
(auch nur einseitig) stetigen Funktion gemacht werden.
nicht zu einer in 0
(auch nur einseitig) stetigen Funktion gemacht werden.
- Durch Dämpfung der Oszillation von
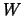 , z.B. durch Multiplikation mit
, z.B. durch Multiplikation mit 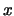 , entsteht eine stetige Funktion:
Da
, entsteht eine stetige Funktion:
Da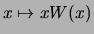 für
für 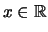 .
.
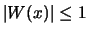 für alle
für alle
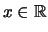 ist, folgt aus
ist, folgt aus
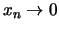 stets
stets
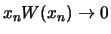 .
.
- Später werden wir statt der Zackenfunktion die
periodischen Funktionen
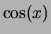 oder
oder 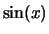 betrachten.
betrachten.
Die damit gebildeten Funktionen
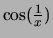 und
und
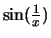 verhalten sich wie die
Wackelfunktion und sind ebenfalls nicht stetig in 0 fortsetzbar.
verhalten sich wie die
Wackelfunktion und sind ebenfalls nicht stetig in 0 fortsetzbar.
Die Funktionen
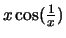 und
und
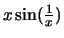 sind dagegen stetig in
sind dagegen stetig in 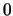 .
.
![[*]](crossref.png)
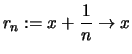 und
und 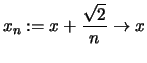 .
.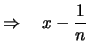
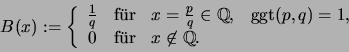
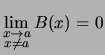 für alle
für alle