



Nächste Seite: Minimum und Maximum
Aufwärts: Reelle Zahlen
Vorherige Seite: Geordnete Körper
Inhalt
Wir arbeiten im allgemeinen nicht mit den Axiomen (O1)-(O3), sondern mit den
entsprechenden Regeln für die Anordnung:
Definition 1.1.7 (Anordnung.)
Wir definieren eine
Anordnung auf
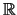
durch
und führen die Notation
ein.
Die Anordnung von
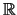 drückt sich geometrisch in der vertrauten Darstellung
der reellen Zahlen auf der Zahlengeraden aus:
Dabei bedeutet
drückt sich geometrisch in der vertrauten Darstellung
der reellen Zahlen auf der Zahlengeraden aus:
Dabei bedeutet 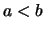 , daß der Punkt
, daß der Punkt 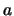 links vom Punkt
links vom Punkt 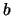 liegt.
liegt.
Die Addition
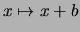 wird zur Verschiebung (Translation) um die
Strecke
wird zur Verschiebung (Translation) um die
Strecke 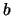 und die Multiplikation
und die Multiplikation
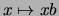 mit einem
mit einem 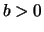 zur
Streckung um den Faktor
zur
Streckung um den Faktor 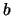 .
.
Man veranschauliche sich die
geometrische Aussage der folgenden Regeln.
Feststellung 1.1.8 (Rechenregeln für Ungleichungen.)
-
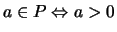 .
.
- Für beliebige reelle Zahlen
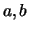 gilt genau eine der drei Relationen
gilt genau eine der drei Relationen
- Aus
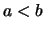 und
und 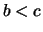 folgt
folgt 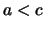 (Transitivität der Anordnung.)
(Transitivität der Anordnung.)
-
Aus
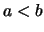
folgt
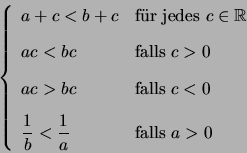
- Man kann Ungleichungen addieren:
- Ungleichungen zwischen positiven Zahlen kann man multiplizieren:
- Es seien
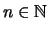 und
und 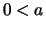 ,
, 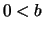 . Dann gilt
. Dann gilt
Zum Beweis siehe
Vorlesung oder [KÖNIGSBERGER, S. 8].
Bezeichnung 1.1.9
Wir führen eine abkürzende Bezeichnung ein:
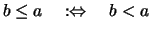
oder
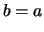
und entsprechend
Bemerkung 1.1.10 (zur Relation
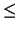
)
Für beliebige reelle Zahlen 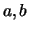 ist
ist
entweder
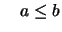
oder
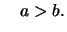
- Die Aussage
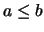 ist die Negation der Aussage
ist die Negation der Aussage 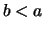 .
.
Man kann eine Aussage 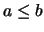 beweisen, indem man den die Annahme
beweisen, indem man den die Annahme 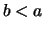 zu einem Widerspruch führt
zu einem Widerspruch führt
- Aus
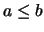 und
und 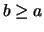 folgt
folgt 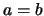 (Antisymmetrie).
(Antisymmetrie).
Diese Schlußweise wird häufig benutzt, um kompliziertere Identitäten zu beweisen, die man nicht durch durch einfaches
Anwenden von Formeln erhalten kann.
- Wenn
gilt, dann ist
Wenn man den Punkt
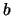 ein wenig nach rechts rückt, läßt sich die Abschätzung oft leichter zeigen
ein wenig nach rechts rückt, läßt sich die Abschätzung oft leichter zeigen




Nächste Seite: Minimum und Maximum
Aufwärts: Reelle Zahlen
Vorherige Seite: Geordnete Körper
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() drückt sich geometrisch in der vertrauten Darstellung
der reellen Zahlen auf der Zahlengeraden aus:
Dabei bedeutet
drückt sich geometrisch in der vertrauten Darstellung
der reellen Zahlen auf der Zahlengeraden aus:
Dabei bedeutet ![]() , daß der Punkt
, daß der Punkt ![]() links vom Punkt
links vom Punkt ![]() liegt.
liegt.
![]() wird zur Verschiebung (Translation) um die
Strecke
wird zur Verschiebung (Translation) um die
Strecke ![]() und die Multiplikation
und die Multiplikation
![]() mit einem
mit einem ![]() zur
Streckung um den Faktor
zur
Streckung um den Faktor ![]() .
.
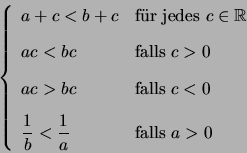
![]() ist
ist
![]() beweisen, indem man den die Annahme
beweisen, indem man den die Annahme ![]() zu einem Widerspruch führt
zu einem Widerspruch führt