Es sei
![]() .
.
- Eine Zahl
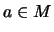 heißt Minimum
von
heißt Minimum
von 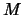 , falls für alle
, falls für alle 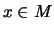 gilt:
gilt:
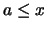 . Man bezeichnet das Minimum von
. Man bezeichnet das Minimum von 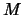 mit
mit 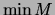 .
.
- Eine Zahl
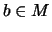 heißt Maximum
von
heißt Maximum
von 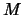 , falls für alle
, falls für alle 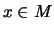 gilt:
gilt:
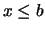 . Man bezeichnet das Maximum von
. Man bezeichnet das Maximum von 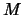 mit
mit 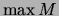 .
.
Es sei
![]() .
.
Ebenso sind Maxima eindeutig bestimmt.
Wenn ![]() ein Maximum hat so ist
ein Maximum hat so ist ![]() das größte Element von
das größte Element von ![]() .
.