Bemerkung. Zu jeder Folge reeller Zahlen kann man
den Limes superior oder
oberen Grenzwert und den Limes inferior oder
unterne Grenzwert in
![]() bilden.
bilden.
Diese beiden Begriffe bilden ein mächtiges Hilfsmittel, um viele Konvergenzaussagen kurz und knapp zu formulieren und auch zu beweisen. Es erfordert aber einige Übung, bis man mit diesem Werkzeug umgehen kann.
In der Lehrbuchliteratur wird der Limes superior bzw. inferior unterschiedlich eingeführt. Diese Definitionen sind alle äquivalent.
Wir wählen eine eher technische, dafür aber leicht anwendbare Definition,
und leiten dann die dazu äquivalenten, anschaulicheren Eigenschaften her.
![[*]](crossref.png) (
(![[*]](crossref.png) ),
),
![[*]](crossref.png) und
und
![[*]](crossref.png) .
.
Zu einer nach oben beschränkten Folge ![]() bilde man
zu jedem
bilde man
zu jedem
![]() die Zahl
die Zahl
![]() .
Die Folge
.
Die Folge ![]() ist monoton fallend.
ist monoton fallend.
Es sei ![]() eine nach oben beschränkte Folge in
eine nach oben beschränkte Folge in
![]() .
Man bilde die monoton fallendende Folge
.
Man bilde die monoton fallendende Folge ![]() durch die Vorschrift:
durch die Vorschrift:
![[*]](crossref.png) und Def.
und Def. ![[*]](crossref.png) )
)
Bemerkung. Analog bildet man den Grenzwert der Infima der Endstücke und nennt ihn den Limes inferior der Folge.
Es sei ![]() eine nach unten beschränkte Folge in
eine nach unten beschränkte Folge in
![]() .
Man bilde die monoton wachsende Folge
.
Man bilde die monoton wachsende Folge
![[*]](crossref.png) und Def.
und Def. ![[*]](crossref.png) )
)
Für den Limes superior gibt es das folgende
![]() -Kriterium:
-Kriterium:
Bemerkung Verschärft man 2.(ii) zu
Beweis .
Bemerkung
Für beschränkte Folge reeller Zahlen liegen
der Limes superior und der Limes inferior in
![]() .
Man kann mit ihrer Hilfe Aussagen über beliebige beschränkte Folgen
formulieren:
.
Man kann mit ihrer Hilfe Aussagen über beliebige beschränkte Folgen
formulieren:
| 1. |
||||
| 2. |
Beweis .
Für eine nach oben unbeschränkte Folge setzt man
Für eine nach unten unbeschränkte Folge setzt man
Bemerkung.
Für jede Folge ![]() gilt also
gilt also
1.
![]()
2.
![]() ist unbeschränkt.
ist unbeschränkt.![]()
Es sei ![]() eine nach oben beschränkte Folge in
eine nach oben beschränkte Folge in
![]() .
.
Wenn
![]() ist, dann ist
ist, dann ist
![]() der größte Häufungswert der Folge
der größte Häufungswert der Folge ![]() .
.
Bemerkung. Dieser Satz wird in vielen Lehrbüchern als Definition des Limes Superior verwendet:
Beweis . 1.
Man setze
![]() .
Es sei
.
Es sei
![]() .
Wir bilden rekursiv eine Teilfolge
.
Wir bilden rekursiv eine Teilfolge
![]() mit folgender Eigenschaft:
mit folgender Eigenschaft:
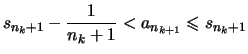 für
für
2. Wenn
![]() eine konvergente Teilfolge ist, so gilt
eine konvergente Teilfolge ist, so gilt
Es seien ![]() und
und ![]() nach oben beschränkte Folgen
in
nach oben beschränkte Folgen
in
![]() und
und ![]() .
Dann gilt:
.
Dann gilt: