



Nächste Seite: Limes superior
Aufwärts: Konvergente Teilfolgen
Vorherige Seite: Konvergente Teilfolgen
Inhalt
Definition 2.7.8
Es sei
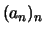
eine Folge in
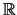
.
Eine Zahl
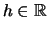
heißt ein Häufungswert der Folge
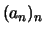
,
wenn es eine Teilfolge von
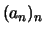
gibt, die gegen
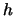
konvergiert.
Beispiel.
- Die Folge
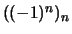 hat die Häufungswerte
hat die Häufungswerte 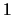 und
und 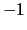 .
.
- Für die Folge im Beispiel
![[*]](crossref.png) ist die Menge der Häufungswerte das Intervall
ist die Menge der Häufungswerte das Intervall ![$ [0,1] $](img1485.png) .
.
Bemerkung 2.7.9 (Existenz von Häufungswerten)
Nach dem Satz von Bolzano-Weierstraß hat jede beschränkte Folge
mindestens einen Häufungswert.
Bemerkung. Für eine konvergente Folge ist der Grenzwert der
einzige Häufungswert.
Es gilt auch die Umkehrung:
Satz 2.7.10
Eine beschränkte Folge ist genau dann konvergent, wenn sie nur
einen Häufungswert hat.
Korollar 2.7.11
Eine beschränkte Folge konvergiert genau dann gegen einen
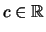
,
wenn jede ihrer Teilfolgen eine Teilfolge hat, die gegen
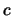
konvergiert.
Beweis des Satzes ![[*]](crossref.png) .
.
- Klar.

- Die Folge
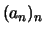 sei beschränkt und
habe genau einen Häufungswert
sei beschränkt und
habe genau einen Häufungswert
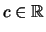 .
.
Annahme: Die Folge konvergiert nicht gegen 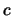 .
Es gibt also es ein
.
Es gibt also es ein
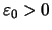 , so daß es zu jedem
, so daß es zu jedem
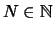 ein
ein
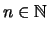 ,
, 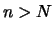 , existiert, für das
, existiert, für das
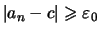 ist.
ist.
Es gibt eine Teilfolge
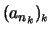 ,
so daß (vgl.
,
so daß (vgl. ![[*]](crossref.png) (3.))
(3.))
Da die Folge
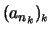 beschränkt ist,
hat sie eine konvergente Teilfolge, die einen anderen Grenzwert als
beschränkt ist,
hat sie eine konvergente Teilfolge, die einen anderen Grenzwert als
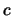 hat.
hat.
Beweis des Korollars ![[*]](crossref.png) .
.
Aus der Vorausetzung des Korollars erhält man, daß jede konvergente
Teilfolge der gegebenen Folge gegen 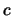 konvergiert.
konvergiert.




Nächste Seite: Limes superior
Aufwärts: Konvergente Teilfolgen
Vorherige Seite: Konvergente Teilfolgen
Inhalt
Analysis1-A.Lambert
2001-02-09
![[*]](crossref.png) ist die Menge der Häufungswerte das Intervall
ist die Menge der Häufungswerte das Intervall ![]() .
Es gibt also es ein
.
Es gibt also es ein
![]() , so daß es zu jedem
, so daß es zu jedem
![]() ein
ein
![]() ,
, ![]() , existiert, für das
, existiert, für das
![]() ist.
ist.
![]() ,
so daß (vgl.
,
so daß (vgl. ![[*]](crossref.png) (3.))
(3.))
![]() beschränkt ist,
hat sie eine konvergente Teilfolge, die einen anderen Grenzwert als
beschränkt ist,
hat sie eine konvergente Teilfolge, die einen anderen Grenzwert als
![]() hat.
hat.
![]() konvergiert.
konvergiert.