Integral von Regelfunktionen

Feststellung 3.1.14   Es seien $I$ ein kompaktes Intervall und $f\in\mathcal{R}(I)$. Für jede Folge $(t_n)_n$ von Treppenfunktionen auf $I$, die gleichmäßig auf $I$ gegen $f$ konvergiert, existiert der Grenzwert

$$\textstyle \lim\limits_{n\to\infty}\int_{I} t_n$$   .$$$$

Dieser Grenzwert hängt nicht von der Wahl der approximierenden Folge ab.

Beweis . Da die Folge $(t_n)_n$ gleichmäßig auf $I$ gegen $f$ konvergiert, gilt das Cauchy-Kriterium

$$\forall\varepsilon >0\ \exists n_0\in\mathbb{N}\ \forall n,m\geqslant n_0\ :\ \Vert f_n-f_m\Vert<\varepsilon$$   .$$$$

Nach Korollar gilt

$$\textstyle \Bigl\vert\, \int\limits_{[a,b]} t_n - \int\limits_{[a,b]}t_m \Bigr\vert \leqslant (b-a)\,\Vert t_n-t_m \Vert$$   .$$$$

Also ist auch die Folge $\bigl( \int\limits_{[a,b]} t_n \bigr)_n$ der Integrale eine Cauchyfolge und somit konvergent.

Nach dem Reißverschlußprinzip konvergiert für jede andere Folge $(\tilde{t}_n)_n$ von Treppenfunktionen, die gleichmäßig gegen $f$ konvergiert, die Folge $\bigl( \int\limits_{[a,b]} \tilde{t}_n \bigr)_n$ der Integrale gegen den gleichen Grenzwert.

Bemerkung. Nach Satz gibt es zu jeder Regelfunktion $f$ auf einem kompakten Intervall eine Folge $(t_n)_n$ von Treppenfunktionen, die gleichmäßig gegen $f$ konvergiert.

Nach Feststellung konvergiert die Folge $(\int\limits_{[a,b]}\! t_n)_n$ der Integrale gegen einen Grenzwert, der unabhängig von der gewählten Folge von Treppenfunktionen ist.

Wir definieren diesen Grenzwert als Integral von $f$:

Definition 3.1.15 (Integral für Regelfunktionen)  

Es sei $f: [a,b] \rightarrow \mathbb{R}$ eine Regelfunktion. Man erklärt das Integral von $f$ als Grenzwert der Integrale einer Folge $(t_n)_n$ von Treppenfunktionen, die auf $[a,b]$ gleichmäßig gegen $f$ konvergiert:

$$\textstyle \int\limits_{[a,b]}\! f :=\lim\limits_{n\to\infty}\int\limits_{[a,b]}\! t_n$$   .$$$$

Satz 3.1.16 (Eigenschaften des Regel-Integrals)  

1. Das Integral erfüllt die Axiome

   Intervall-Additivität,

   Monotonie,

   Eichung.

   Es ist durch diese Axiome eindeutig bestimmt.
2. Das Integral ist linear: Für Regelfunktionen $f$, $g$ auf einem kompakten Intervall $I$ und $\lambda$, $\mu \in \mathbb{R}$ gilt
   $$\textstyle \int\limits_{I}(\lambda f + \mu g) = \lambda\int\limits_{I} f \ + \ \mu\int\limits_{I} g$$   .$$$$

3. Das Integral ist beschränkt: Für eine Regelfunktion $f$ auf einem kompakten Intervall gilt:
   $$\textstyle \bigl\vert \int\limits_{I} f \bigr\vert \leqslant (b-a)\,\Vert f\Vert$$.$$$$

Beweis .

1. Inervall-Additivitat:

   überträgt sich von den Treppenfunktionen (vgl. Satz ) unmittelbar auf die Grenzwerte.

   Monotonie:

   Es seien $f$, $g$ Regelfunktionen auf $[a,b]$ und es gelte $f\leqslant g$. Nach Korollar gibt es eine monoton wachsende Folge $(s_n)_n$, die gleichmäßig gegen $f$ konvergiert und eine monoton fallende Folge $(t_n)_n$ von Treppenfunktionen, die gleichmäßig gegen $g$ konvergiert.

   Dann ist $s_n \leqslant f \leqslant g \leqslant t_n$ und folglich

   $$\textstyle \int\limits_{[a,b]}\! f = \lim\limits_{n\to\infty}\int... ... :=\lim\limits_{n\to\infty}\int\limits_{[a,b]}\! t_n = \int\limits_{[a,b]}\! g$$   .$$$$

   Eichung:

   Die Eichung gilt für Treppenfunktionen.

   Eindeutigkeit:

   Es gibt eine monoton wachsende Folge $(s_n)_n$ und eine monoton fallende Folge $(t_n)_n$ von Treppenfunktionen, die gleichmäßig gegen $f$ konvergieren. Aus der Monotonie des Integrals folgt nun die Eindeutigkeit.

2. Die Linearität des Integrals von Treppenfunktionen überträgt sich unmittelbar auf die Grenzwerte (vgl. )
3. Die Beschränktheit des Integrals von Treppenfunktionen überträgt sich unmittelbar auf die Grenzwerte. (vgl. )

Korollar 3.1.17 (Beschränktheit des Integrals)  

1. Es sei $[a,b] \subset \mathbb{R}$ ein kompaktes Intervall. Für das Integral zweier Regelfunktionen $f$, $g\in\mathcal{R}([a,b])$ gilt:
   $$\textstyle \Bigl\vert\, \int\limits_{[a,b]} f - \int\limits_{[a,b]}g \Bigr\vert \leqslant (b-a)\,\Vert f-g \Vert$$   .$$$$

2. Konvergiert eine Funktionenfolge $(f_n)_n$ in $\mathcal{R}([a,b])$ gleichmäßig auf $[a,b]$ gegen $f$, dann ist $f\in \mathcal{R}([a,b])$ und es gilt
   $$\textstyle \int\limits_{[a,b]}f = \int\limits_{[a,b]} \lim\limits_{n\to\infty} f_n = \lim\limits_{n\to\infty} \int\limits_{[a,b]}f_n$$

Bemerkung 3.1.18 (Endlich viele Punkte)  

1. Eine Funktion $\phi:[a,b]\rightarrow \mathbb{R}$, die nur in endlich vielen Punkten einen Wert ungleich Null hat, ist eine Treppenfunktion mit $\int\limits_{[a,b]} \phi = 0$.

2. Es sei $f\in \mathcal{R}([a,b])$. Ändert man $f$ in endlich vielen Punkten beliebig ab, so ändert sich der Wert des Integrals nicht:

$$\textstyle \int\limits_{[a,b]} (f+\phi) \int\limits_{[a,b]} f$$   .$$$$

Bemerkung. Unter einer Tranlation versteht man die Abbildung

$$\mathbb{R}\ni x \mapsto x+c$$,$$$$

wobei $c \in \mathbb{R}$ eine Konstante ist.

An der Eichungsformel sieht man, daß das Integral einer Treppenfunktion invariant unter Tranlationen ist. Dies überträgt sich dann auf Regelfunktionen:

Bemerkung 3.1.19 (Translationsinvarianz)  

Das Integral ist translationsinvariant. Für $f\in \mathcal{R}([a,b])$ und $c \in \mathbb{R}$ gilt:

$$\int_a^b f(x)\,dx = \int_{a+c}^{b+c} f(x-c)\,dx$$

Bemerkung. Eine affine Funktion hat die Form

$$\mathbb{R}\ni x \mapsto cx+d$$   mit Konstanten $c,d\in\mathbb{R}$.$$$$

Die folgende Transformationsformel ist ein Spezialfall der Substitutionsformel für Integrale.

Lemma 3.1.20 (Affine Transformationen)  

Gegeben sei eine affine Funktion $g: x\mapsto cx+d$, $x \in \mathbb{R}$ mit Konstanten $c$, $d\in\mathbb{R}$, $c\not=0$, ein kompaktes Intervall $I$ und $J=g(I)$. Für $f\in\mathcal{R}(J)$ gilt:

$$\textstyle \int\limits_{g(I)} f = \vert c\vert\,\int\limits_{I} f\circ g$$   .$$$$

Man beachte, daß auf der rechten Seite der Betrag von $c$ steht. Ist $I = [a,b]$ so lautet die Formel in Differential-Schreibweise:

$$\int_{g(a)}^{g(b)} f(y)\,dy = \int_a^b f(g(x))\cdot c\,dx$$   .$$$$

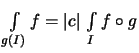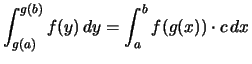Beweis . Es reicht die Transformationsformel für Treppenfunktionen zu zeigen. Durch Grenzwertbildung folgt sie dann für Regelfunktionen.

Wegen der Intervall-Additivität des Integrals reicht es, die Formel für konstante Funktionen $f= K$ zu zeigen.

Es sei $I = [a,b]$.

Wir betrachten zunächst den Fall $c>0$. Dann ist $g(a) < g(b)$ und es gilt

$$\textstyle \int\limits_{g(I)} f = K(g(b)-g(a)) = K\,c\,(b-a) = c \int\limits_{[a,b]} f\circ g$$   .$$$$

Im Falle $c<0$ ist $g(a) > g(b)$ und es gilt

$$\textstyle \int\limits_{g(I)} f = K(g(a)-g(b)) = K\,c\,(a-b) = -c \int\limits_{[a,b]} f\circ g$$   .$$$$