1. Es sei
![]() stetig und streng monoton
wachsend mit Umkehrfunktion
stetig und streng monoton
wachsend mit Umkehrfunktion
![]() .
Dann gilt
.
Dann gilt
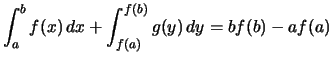 .
.![$\displaystyle \textstyle
\int\limits_{[a,b]}f
- \int\limits_{[f(b),f(a)]}\!\!\!\! g = bf(b)-af(a)$](img2474.png) .
.Bemerkung. Man veranschauliche die Aussage des folgenden Satzes und auch den Beweis mit einer Zeichnung.
1. Es sei
![]() stetig und streng monoton
wachsend mit Umkehrfunktion
stetig und streng monoton
wachsend mit Umkehrfunktion
![]() .
Dann gilt
.
Dann gilt
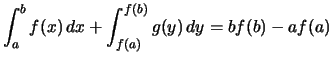 .
.![$\displaystyle \textstyle
\int\limits_{[a,b]}f
- \int\limits_{[f(b),f(a)]}\!\!\!\! g = bf(b)-af(a)$](img2474.png) .
.
Beweis . 1: ![]() streng monoton wachsend:
Es seien
streng monoton wachsend:
Es seien
![]() ,
,
![]() ,
,
![]() .
Man erhält eine Einteilung
.
Man erhält eine Einteilung
![]() des Bildes.
Man addiere die Riemannschen Summen von
des Bildes.
Man addiere die Riemannschen Summen von ![]() und
und ![]() :
:
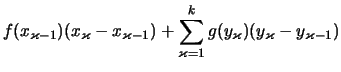 |
||
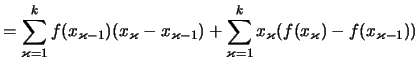 |
||
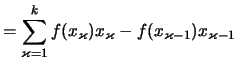 |
||
2: ![]() streng monoton fallend:
Es seien
streng monoton fallend:
Es seien
![]() ,
,
![]() ,
,
![]() .
Man erhält eine Einteilung
.
Man erhält eine Einteilung
![]() von
von
![]() .
Man subtrahiere die Riemannschen Summen von
.
Man subtrahiere die Riemannschen Summen von ![]() und
und ![]() :
:
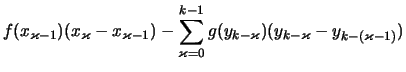 |
||
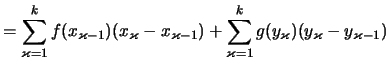 |
||
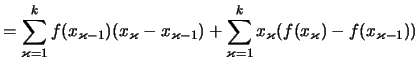 |
||
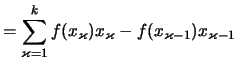 |
||
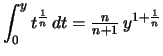 .
.Beweis . Für ![]() und
und ![]() gilt
gilt
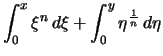 ,
,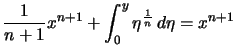
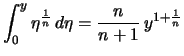 .
.
Übung.
Und schließlich
![]() für
für
![]() .
.
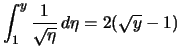 .
.
Bemerkung. Die Exponentialfunktion
![]() ist ein unbestimmtes Integral von sich selbst.
Man schreibt abkürzend:
ist ein unbestimmtes Integral von sich selbst.
Man schreibt abkürzend:
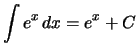 .
.
Beweis . Für ![]() und
und
![]() gilt
gilt
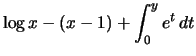 |
||
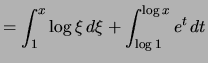 |
||
Im Fall ![]() gilt eine analoge Rechnung für
gilt eine analoge Rechnung für ![]() :
:
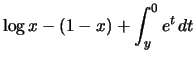 |
||
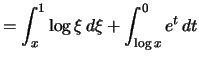 |
||
Durch partielle Integration erhalt man
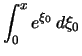 |
||
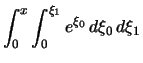 |
||
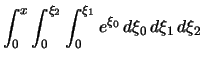 |
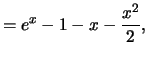 |
|
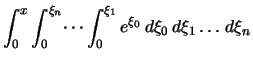 |
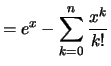 . . |
![[*]](crossref.png) )
)
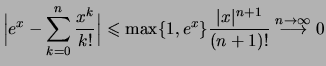 .
.