Für zwei Funktionen ![]() ,
,
![]() bezeichne
bezeichne
Bemerkung. Die Formel der partiellen Integration gilt für
beliebige, fest gewählte Stammfunktionen ![]() von
von ![]() und
und ![]() von
von ![]() (vgl. Definition
(vgl. Definition ![[*]](crossref.png) ).
).
Bemerkung.
Nach Bemerkung ![[*]](crossref.png) kann man
die Treppenfunktionen
kann man
die Treppenfunktionen ![]() und
und ![]() in den Sprungstellen
abändern, ohne die Stammfunktionen und die Werte der Integrale
in den Sprungstellen
abändern, ohne die Stammfunktionen und die Werte der Integrale
![$\displaystyle \int\limits_{[a,b]}F\,g$](img2427.png) und
und![$\displaystyle \quad
\int\limits_{[a,b]}g\,F
$](img2428.png)
Wir können für den Beweis also ohne Einschränkung annehmen,
daß ![]() rechtsseitig und
rechtsseitig und ![]() linksseitig stetig ist.
linksseitig stetig ist.
Beweis . Es sei ![]() eine Treppenfunktion mit Stammfunktion
eine Treppenfunktion mit Stammfunktion ![]() und
und ![]() eine Treppenfunktion mit Stammfunktion
eine Treppenfunktion mit Stammfunktion ![]() .
.
Nach der Vorbemerkung können wir ohne Einschränkung annehmen, daß
![]() rechtsseitig und
rechtsseitig und
![]() linksseitig stetig ist.
linksseitig stetig ist.
Die Integrale
![]() und
und
![]() approximiert man durch
Riemannscher Summen zu Zerlegungen
approximiert man durch
Riemannscher Summen zu Zerlegungen
![[*]](crossref.png) ).
).
Man kann die Zerlegungspunkte zugleich als Stützpunkte wählen.
Zu
![]() gibt es eine
gibt es eine ![]() , so daß aus
, so daß aus
![]() stets folgt:
stets folgt:
![$\displaystyle \textstyle \bigl\vert \int\limits_{[a,b]}F\,g - \sum_{\varkappa=1...
...arkappa)g(x_\varkappa) \,(x_\varkappa-x_{\varkappa-1}) \bigr\vert < \varepsilon$](img2432.png) |
|
![$\displaystyle \textstyle \bigl\vert \int\limits_{[a,b]}f\,G - \sum_{\varkappa=1...
...-1})G(x_{\varkappa-1}) \,(x_\varkappa-x_{\varkappa-1}) \bigr\vert < \varepsilon$](img2433.png) |
Man kann ohne Einschränkung solche Zerlegungen ![]() wählen,
auf deren offenenen Teilintervallen
wählen,
auf deren offenenen Teilintervallen
![]() und
und
![]() konstant sind,
anderenfalls füge man die Sprungstellen von
konstant sind,
anderenfalls füge man die Sprungstellen von ![]() und
und ![]() als weitere Zerlegungspunkte hinzu.
als weitere Zerlegungspunkte hinzu.
Da ![]() rechtsseitig und
rechtsseitig und ![]() linksseitig stetig ist, folgt:
linksseitig stetig ist, folgt:
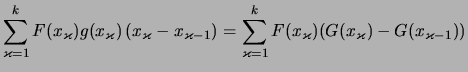 |
||
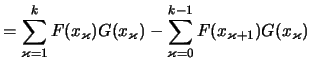 |
||
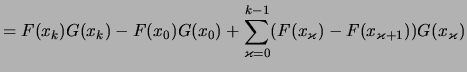 |
||
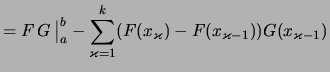 |
||
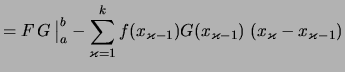 |
![$ \textstyle
\int\limits_{[a,b]} F\,g
= F\,G\,\bigr\vert _a^b - \int\limits_{[a,b]} f\,G
$](img2449.png) .
.
Wir berechnen induktiv
die Stammfunktionen zu den Potenzen ![]() :
:
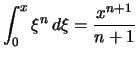 für
für
Beweis .
 .
. .
.
Daraus folgt
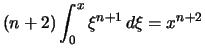 .
.
Bezeichnung.
Eine Funktion ![]() heißt unbestimmtes Integral
einer Funktion
heißt unbestimmtes Integral
einer Funktion ![]() , wenn für alle
, wenn für alle ![]() ,
, ![]() im Definitionsbereich von
im Definitionsbereich von ![]() und
und ![]() gilt:
gilt:
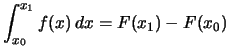
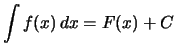 .
.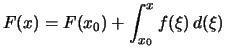 .
.![$\displaystyle \textstyle
\int\limits_{[a,b]} F\,g + \int\limits_{[a,b]} f\,G
= F\,G\,\bigr\vert _a^b
$](img2460.png)
Beispiel.
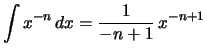 für
für
![[*]](crossref.png) (3.)
(3.)
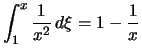 .
.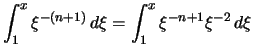 |
||
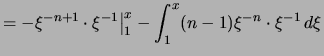 . . |
Daraus folgt
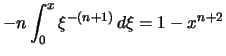 .
.
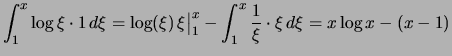 .
.