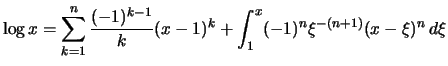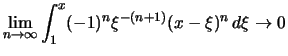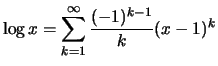![$\displaystyle \textstyle
m \int\limits_{[a,b]}\! g
\leqslant \int\limits_{[a,b]}\! fg
\leqslant M \int\limits_{[a,b]}\! g$](img2537.png) .
.
![$\displaystyle \textstyle
m \int\limits_{[a,b]}\! g
\leqslant \int\limits_{[a,b]}\! fg
\leqslant M \int\limits_{[a,b]}\! g$](img2537.png) .
.
Bemerkung. Aus dem Zwischenwertsatz
![[*]](crossref.png) folgt nun:
folgt nun:
Bezeichnung. Für ![]() ,
,
![]() und
feste
und
feste ![]() ,
,![]() bilde man die
iterierten Stammfunktionen:
bilde man die
iterierten Stammfunktionen:
Beweis . ![]() Klar.
Klar.
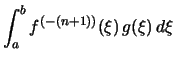
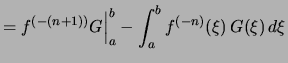 |
||
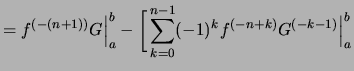 |
||
![$\displaystyle \strut\qquad + (-1)^{n}\int_a^b f(\xi)\,G^{(-n)}(\xi)\,d\xi \biggr]$](img2559.png) |
||
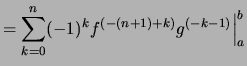 |
||
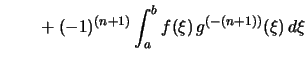 . . |
Bemerkung. Formuliert man die folgende Feststellung mit Ableitungen statt mit Stammfunktionen, so heißt dies Resultat Taylorformel mit Restglied und ist einer der wichtigsten Sätze der Analysis:
Es seien
![]() ein Intervall,
ein Intervall,
![]() und
und ![]() .
Für eine
.
Für eine ![]() -ten Stammfunktion
-ten Stammfunktion ![]() von
von
![]() und
und ![]() gilt:
gilt:
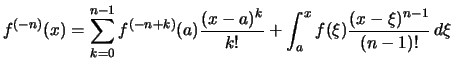 .
.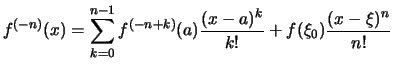 .
.![[*]](crossref.png) )
)
Beweis . Setzt man in Feststellung
![[*]](crossref.png)
![]() und
und ![]() so erhält man die Stammfunktionen
so erhält man die Stammfunktionen
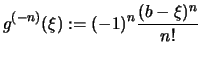 .
.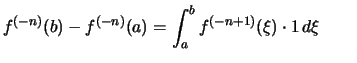 |
|
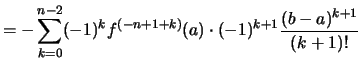 |
|
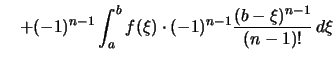 . . |
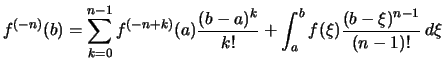 .
.
Für ![]() gilt
gilt