Es seien ![]() ein offenes Intervall,
ein offenes Intervall,
![]() und
und
![]() ein
unbestimmtes Integral von
ein
unbestimmtes Integral von ![]() , d.h.
, d.h.
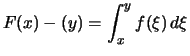 für alle
für alle Bemerkung. Wir betrachten in diesem Abschnitt Funktionen auf einem Intervall, die in jedem Punkt des Intervalls differenzierbar sind.
Es seien ![]() ein offenes Intervall,
ein offenes Intervall,
![]() und
und
![]() ein
unbestimmtes Integral von
ein
unbestimmtes Integral von ![]() , d.h.
, d.h.
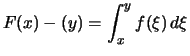 für alle
für alle
Beweis (Ableitung einer Stammfunktion).
Da ![]() im Punkt
im Punkt ![]() stetig ist, existiert
zu
stetig ist, existiert
zu
![]() ein
ein ![]() , so daß
, so daß
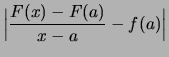 |
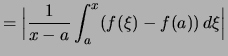 |
|
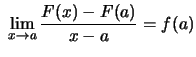 .
.
Beweis . Man schreibe ![]() und
und ![]() als Stammfunktionen
und benutze die Feststellung
als Stammfunktionen
und benutze die Feststellung ![[*]](crossref.png) :
:
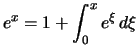 für
für
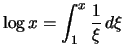 für
für
Bemerkung Das folgende Beispiel zeigt, daß unbestimmte Integrale von Regelfunktionen und überall differenzierbare Funktionen verschieden Klassen sind.
Bemerkung. Man zeichne ein Bild eines `glatten' Funktionsgraphen mit den unten angegebenen Eigenschaften.
Die Funktion hat ein Maximum oder ein Minimum im Inneren des Intervalls.
In diesem Punkt muß die Tangente waagerecht verlaufen.
Es sei
![]() stetig und die Einschränkung
stetig und die Einschränkung
![]() sei auf dem offenen Intervall
sei auf dem offenen Intervall ![]() differenzierbar.
differenzierbar.
Wenn
![]() ist, so gibt es ein
ist, so gibt es ein
![]() mit
mit
![]() .
.
ROLLE, MICHEL (1652-1719)
Bemerkung. Die obige Voraussetzung an eine Funktion ![]() wird uns noch häufig begegnen. Wir sagen kurz:
wird uns noch häufig begegnen. Wir sagen kurz:
![]() ist stetig auf dem Intervall
und im Inneren (des Intervalls) differenzierbar.
ist stetig auf dem Intervall
und im Inneren (des Intervalls) differenzierbar.
Beweis (Satz von Rolle).
Sei etwa
![]() un
un ![]() ein Minimum.
Dann ist
ein Minimum.
Dann ist
![$\displaystyle \frac{ f(x)-f(\xi) }{ x-\xi }\ \left\{\begin{array}{ll} \leqslant...
... \geqslant 0 &\text{f\uml ur \( x>\xi \), \( x\in [a,b] \),} \end{array}\right.$](img2757.png) |
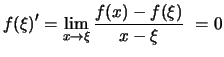 .
.
Es sei
![]() stetig und die Einschränkung
stetig und die Einschränkung
![]() sei auf dem offenen Intervall
sei auf dem offenen Intervall ![]() differenzierbar.
differenzierbar.
Dann gibt es ein
![]() , so daß
, so daß
LAGRANGE, JOSEPH, LOUIS (1736-1813)
Bemerkung
Geometrisch besagt der Mittelwertsatz, däß die Tangente im
Punkte ![]() an den Graphen von
an den Graphen von ![]() dieselbe
Steigung hat, wie die Sekante durch die Punkte
dieselbe
Steigung hat, wie die Sekante durch die Punkte
![]() und
und ![]()
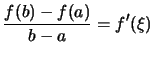 .
.
Bemerkung. Der Mittelwertsatz gilt nur für reellwertige Funktionen und läßt sich nicht auf vektorwertige Funktionen übertragen.
Häufig benötigt man aber nur eine aus dem Mittelwertsatz folgende Abschätzung, den Schrankensatz. Diese Methode, den Mittelwertsatz zum Abschätzen einzusetzen, läßt sich weitgehend verallgemeinern.
Es sei ![]() ein Intervall und
ein Intervall und
![]() stetig und
differenzierbar im Innern von
stetig und
differenzierbar im Innern von ![]() .
.
Wenn die Ableitung beschränkt ist:
Beweis (Mittelwertsatz).
Der Fall ![]() ist trivial. Es sei also
ist trivial. Es sei also ![]() :
:
Subtrahiert man die Sekantengleichung von der Funktion
![]() , so erhält man eine Funktion
, so erhält man eine Funktion ![]() , auf die
man den Satz von Rolle anwenden kann:
, auf die
man den Satz von Rolle anwenden kann:
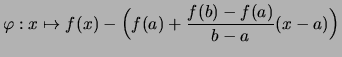 .
.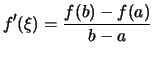 .
.
Bemerkung. Aus dem Mittelwertsatz folgt unmittelbar das folgende einfache, aber sehr bedeutsame Korollar:
Es sei ![]() ein Intervall und
ein Intervall und
![]() stetig und differenzierbar im Innern von
stetig und differenzierbar im Innern von ![]() .
.
Wenn die Ableitung verschwindet