$\mathit{MIN}$ und $\mathit{MAX}$

 Sei E ein normierter Raum. Unter allen Operatorraumnormen auf E, die auf der ersten Stufe mit der gegebenen Norm übereinstimmen, gibt es eine größte und eine kleinste. Die dadurch gegebenen matrixnormierten Räume nennt man     ${\mathit{MAX}(E)}$ und     ${\mathit{MIN}(E)}$. Sie sind charakterisiert durch die folgende universelle Abbildungseigenschaft:¹³ Für jeden matrixnormierten Raum X ist isometrisch

$$M_1(\mathit{CB}(\mathit{MAX}(E),X)) = B(E,M_1(X))$$

und

$$M_1(\mathit{CB}(X,\mathit{MIN}(E))) = B(M_1(X),E) \mbox{.}$$

Es ist [Ble92a]

$$\begin{eqnarray*}\mathit{MIN}(E)^*& \stackrel{\mathrm{cb}}{=}& \mathit{MAX}(E^*)... ...{MAX}(E)^*& \stackrel{\mathrm{cb}}{=}& \mathit{MIN}(E^*)\mbox{.} \end{eqnarray*}$$

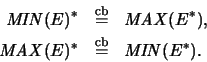
Ist ${\mathrm{dim}}(E) = \infty$, so ist

$$\mathrm{id}_E:\mathit{MIN}(E)\rightarrow \mathit{MAX}(E)$$

nicht vollständig beschränkt [Pau92, Cor. 2.13].¹⁴