- ...
 .1
.1
-
Folgende zwei schwächere Axiomatisierungen sind zu dieser äquivalent:
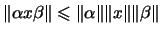
für alle
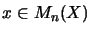
,
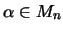
,
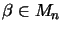
,
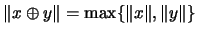
für alle
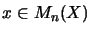
,
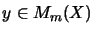
,
wie in der Literatur häufig gefordert wird, sowie
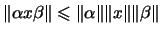
für alle
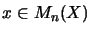
,
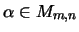
,
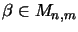
,
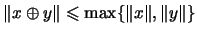
für alle
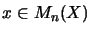
,
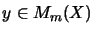
,
was in der Konvexitätstheorie gewisse Vorteile bietet.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... NAME="def:Operatorraum"> Operatorraum2
-
Die Begriffe matrixnormierter Raum und Operatorraum werden in der
Literatur zum Teil anders und nicht ganz einheitlich verwandt. Wir schlagen die hier
erstmals so gebrauchte Terminologie vor in Analogie zu normierter Raum
und
Banachraum.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ......).3
-
In der Literatur wird der normierte Raum M1(X),
die Grundstufe, meist ebenfalls mit
X bezeichnet. Wir meinen, daß eine genauere Unterscheidung manchmal
hilfreich ist.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sind.4
-
Das heißt:
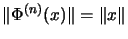 für alle
für alle
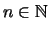 ,
,
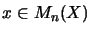 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sind.5
-
Das heißt:
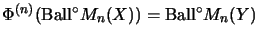 für alle
für alle
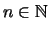 .
Dabei ist
.
Dabei ist
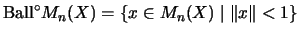 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... formulieren.6
-
Die Normen auf den Matrizenstufen Mn(X) werden zu einer Abbildung
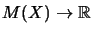 .
Die Amplifikationen von
.
Die Amplifikationen von
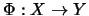 kann man zu einer einzigen Abbildung
kann man zu einer einzigen Abbildung
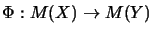 zusammenfassen. Es ist
zusammenfassen. Es ist
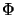 ist vollständig isometrisch, falls
ist vollständig isometrisch, falls
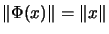 für alle
für alle 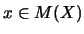 ,
und
,
und 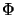 ist eine vollständige
Quotientenabbildung, falls
ist eine vollständige
Quotientenabbildung, falls
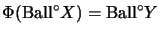 .
Dabei ist
.
Dabei ist
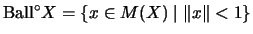 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wir7
-
In der Literatur wird meist das Symbol Mp(X) sowohl für den
Operatorraum mit Grundstufe Mp(X) als auch für die p-te Stufe
des Operatorraumes X verwendet.
Wir meinen aber, daß die Unterscheidung von
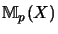 und Mp(X) hilfreich ist, z.B. bei der Definition der Operatorraumstruktur
von CB(X,Y).
und Mp(X) hilfreich ist, z.B. bei der Definition der Operatorraumstruktur
von CB(X,Y).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... NAME="def:dual"> Dual8
- In der Literatur findet sich mitunter der
Begriff
Standarddual [Ble92a].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....9
-
Die Norm eines matrixnormierten Raumes X ist durch die Einheitskugel
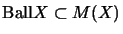 bestimmt. Es gilt:
bestimmt. Es gilt:
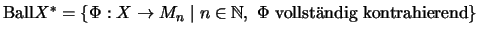 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 2.5]10
-
Daraus folgt die vollständige Isometrie via
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... folgt11
-
Unter Benutzung obiger Formel
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1.1].12
-
Die Isometrie auf den Matrizenstufen folgt aus der Isometrie auf der Grundstufe und der
obigen Formel
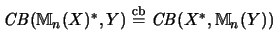 :
:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...:13
-
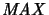 ist also die Linksadjungierte und
ist also die Linksadjungierte und
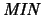 die Rechtsadjungierte
des Vergißfunktors, der einem Operatorraum X den Banachraum M1(X) zuordnet.
die Rechtsadjungierte
des Vergißfunktors, der einem Operatorraum X den Banachraum M1(X) zuordnet.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 2.13].14
- Paulsen baut seinen Beweis
auf einer falschen
Abschätzung für die Projektionskonstante des endlichdimensionalen
Hilbertraums; die umgekehrte Abschätzung ist richtig [Woj91, p. 120],
aber dort nutzlos.
Die Lücke füllt sich dennoch leicht [Lam97, Thm. 2.2.15], durch das Einbringen des
berühmten Satzes von Kadets-Snobar:
Die Projektionskonstante eines n-dimensionalen Banachraums ist
kleinergleich
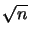 [KS71].
[KS71].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... treten15
- Philologische Fußnote: Der
Autor ist sich der philosophischen Tragweite seiner Ausdrucksweise, die in dem Prädikat
,,zutage treten`` zutage tritt, in aller Konsequenz bewußt und weiß sich im Spannungsfeld zwischen
reinem Konstruktivismus und platonisch fundiertem Realismus. Um an dieser Stelle seine Position, welche die Mathematik als eine in
der Tat partiell real existente, zugleich aber vom denkenden Individuum entworfene Wissenschaft begreift, klar zutage treten zu
lassen, sei denn im folgenden in stetem Bezug auf das unter ,,Matière à pensée`` publizierte Gespräch zwischen
Alain Connes und
Jean-Pierre Changeux [CC92] das von ihm favorisierte Bild der Mathematik in kurzen Strichen skizziert.
In der Sicht Alain Connes' stellt die Mathematik eine vom Menschen unabhängige, wenngleich geistige, so doch gleichsam greifbare
Wirklichkeit dar, die in ihrer ontologischen Basis der platonischen Ideenwelt vergleichbar ist. Connes bekennt sich somit zu einem
beinahe radikal zu nennenden Realismus; die Aufgabe des Mathematikers besteht hiernach, pointiert formuliert, einzig und allein
darin, die vorhandene ,,harte Realität`` zu entdecken.
Jean-Pierre Changeux setzt diesem das Bild des rein erfindenden Denkers entgegen. In den Augen des Neurobiologen existiert die von
Alain Connes als realiter vorfindbar beschriebene und als solche dem Forscher erfahrbare Welt lediglich in den Hirnwindungen, in den
Synapsen besagten Denkers. Diese konstruktivistische Perspektive versteht Mathematik als reine Fiktion und ersetzt die platonische
Ontologie gleichsam durch biologische Substanz.
Der Verfasser nun wagt es weder, einer der beiden Positionen vollends zu widersprechen, noch aber vermag er sich ihrer Radikalität
anzuschließen. Er folgt vielmehr einem Kompromiß zwischen beiden Ansätzen, welchen der in seinem Verständnis fundamentale Punkt
der Axiomatik stiftet. Für ihn ist Mathematik in und bis zum (vorläufigen) Abschluß der Axiomatik in sich kohärente Erfindung,
wobei einzig die Logik der Fiktion die Schranken weist, in dem Maße wie sie als Garant der inneren Kohärenz auftritt - den
Schlußpunkt der Axiomatik freilich setzt zunächst desgleichen die freie Erfindung.
Unter diesen Prämissen gibt es prinzipiell viele verschiedene ,,Mathematiken``: quot capita, tot senses.
Ist jedoch einmal das axiomatische Fundament gelegt, so bleibt dem Forscher allein, die hierdurch erschaffene, obschon dem Schöpfer
selbst noch
unbekannte Welt zu erkunden: er kann nur noch entdecken, was er schon geschaffen, dieses Descartessche ,,Spiel des
menschlichen
Geistes mit sich selbst`` spielen, dessen Regeln er selbst aufgestellt hat. - Auf eine
genaue Definition, also Abgrenzung, der
Begriffe ,,Regel``, ,,Postulat`` sowie ,,Axiom`` wird hier aus Platzgründen bewußt verzichtet.
Endlich lehrt uns Gödel, daß auch dieses Spiel seinerseits sich einem Wechselspiel zwischen Erfinden und Entdecken unterordnet,
insofern als gewisse Entdeckungen weitere Axiome fordern, die ihrerseits neue Entdeckungen hervorbringen. Ein wechselseitig sich
bedingender und befruchtender Dualismus zwischen Konstruktivismus und Realismus zeichnet so ein in stetem Wandel begriffenes
Bild der Mathematik.
Abschließend sei folgendem Vermerk noch Raum gegriffen, daß die hier vertretene Sicht der Mathematik ex post greift; sie weiß sich ahistorisch.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gebildet.16
- Es bezeichne M* den (eindeutigen) Prädual von M.
Dann gilt die
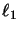 -direkte Summen-Zerlegung
-direkte Summen-Zerlegung
in normale (d.h. w*-stetige) und singuläre Funktionale.
[In der Literatur findet man
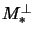 statt M*s, passend zu
statt M*s, passend zu
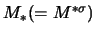 .]
Analog heißt
.]
Analog heißt
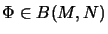 ,
M, N von Neumann-Algebren, normal (d.h.
w*-w*-stetig), falls
,
M, N von Neumann-Algebren, normal (d.h.
w*-w*-stetig), falls
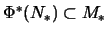 ,
und singulär, falls
,
und singulär, falls
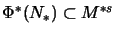 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Amplifikation17
- In der Literatur, etwa [BRS90, p. 190],
wird häufig
die bilineare Amplifikation
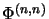 als die Amplifikation bezeichnet
und mit
als die Amplifikation bezeichnet
und mit
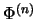 notiert.
notiert.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 .18
.18
- Zur Erklärung der vollständigen Beschränktheit von bilinearen
Abbildungen genügt es, nur die
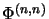 statt aller
statt aller
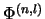 zu betrachten; dies findet man
häufig in der Literatur über
vollständig beschränkte bi- und analog multilineare Abbildungen [BRS90, p. 190],
[CES87, p. 281].
zu betrachten; dies findet man
häufig in der Literatur über
vollständig beschränkte bi- und analog multilineare Abbildungen [BRS90, p. 190],
[CES87, p. 281].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 19
- Zur Bildung der Operatorräume
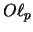 siehe das Kapitel über
komplexe Interpolation .
siehe das Kapitel über
komplexe Interpolation .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...öbste20
-
D.h., die injektive Operatorraum-Tensornorm ist die kleinste
Operatorraum-Tensornorm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... feinste21
-
D.h., die projektive Operatorraum-Tensornorm ist die größte
Operatorraum-Tensornorm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 22
-
D.h., wenn
![$
[S_{ij}] \in M_p(\mathit{CB}(X_1,X_2))$](img368.gif) ,
,
![$
[T_{kl}] \in M_q(\mathit{CB}(Y_1,Y_2))$](img369.gif) ,
,
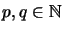 ,
so gilt für den Operator
,
so gilt für den Operator
die Normabschätzung
Anmerkung: Hierin gilt sogar die Gleichheit.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ersetzen.23
-
(2)
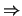 (3),(4):
Die Bedingung (3) ist ein Spezialfall von (2).
Es seien
(3),(4):
Die Bedingung (3) ist ein Spezialfall von (2).
Es seien
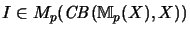 ,
,
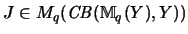 Matrizen, die algebraisch
die identischen Abbildungen der zugrundeliegenden Vektorräume
Mp(X) bzw. Mq(Y) sind.
Nach Voraussetzung (2) gilt
Matrizen, die algebraisch
die identischen Abbildungen der zugrundeliegenden Vektorräume
Mp(X) bzw. Mq(Y) sind.
Nach Voraussetzung (2) gilt
Nun ist
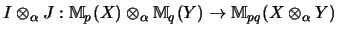 die shuffle-Abbildung aus (4).
die shuffle-Abbildung aus (4).
(3),(4)
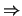 (2):
Wenn
(2):
Wenn
![$
[S_{ij}] \in M_p(\mathit{CB}(X_1,X_2))$](img368.gif) ,
,
![$
[T_{kl}] \in M_q(\mathit{CB}(Y_1,Y_2))$](img369.gif) ,
,
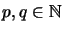 ,
so seien
,
so seien
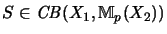 ,
,
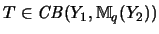 die entsprechenden Operatoren.
Nach (3) gilt
die entsprechenden Operatoren.
Nach (3) gilt
Wenden wir nun die shuffle-Abbildung
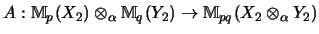 an, so folgt aus (4)
an, so folgt aus (4)
Also ist
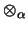 allgemein vollständig kontrahierend.
allgemein vollständig kontrahierend.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(i)-(iii).24
-
Äquivalent zu (i)-(iii) ist, daß die bilinearen Abbildungen
allgemein vollständig kontrahierend
sind.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... NAME="sec:injektivesORTP"> injektives25
- Andere Bezeichnungen sind räumliches
Operatorraum-Tensorprodukt
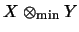 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)=1.26
- Eine Charakterisierung exakter C*-Algebren findet sich in
[Kir94] und [Kir95].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... definieren27
- Die Abkürzung SK steht für Subspaces of
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...dukt28
-
Wenn
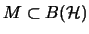 ,
,
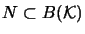 von Neumann-Algebren sind,
dann ist
von Neumann-Algebren sind,
dann ist
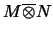 der Abschluß des algebraischen Tensorproduktes
der Abschluß des algebraischen Tensorproduktes
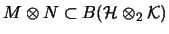 in der schwachen Operatortopologie.
in der schwachen Operatortopologie.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...H-Tensorproduktes
29
- Diese Tensornorm ist auch als
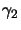 bekannt [Pis86].
bekannt [Pis86].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
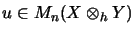 :30
:30
-
Die Definition der
tensoriellen Matrixmultiplikation
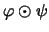 von Abbildungen
von Abbildungen 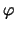 ,
,
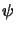 und der der
Amplifikation
der Dualität von Tensorprodukten
ergibt
und der der
Amplifikation
der Dualität von Tensorprodukten
ergibt
für 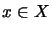 ,
,
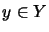 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zeigt:31
-
Algebraisch hat man auf beiden Seiten die gleichen Räume von Matrizen.
Auf der linken Seite erhält man aber die feinere Operatorraumstruktur
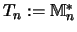 der Spurklasse
der Spurklasse
Dagegen ergibt die rechte Seite die gröbere Operatorraumstruktur Mn der Matrizen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kontrahierend.32
-
Dies folgt aus der der
der Eigenschaft
2
mit den Eigenschaften
3
und
4
von Operatorraum-Tensorprodukten.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... folgern33
-
Dieses Verfahren kann man bereits bei der Herleitung dieser vollständigen
Isometrie anwenden.
Man sieht leicht, daß auf der Grundstufe
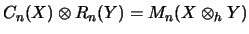 isometrisch gilt.
Hieraus folgt nun die vollständige Isometrie - für alle
isometrisch gilt.
Hieraus folgt nun die vollständige Isometrie - für alle
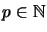 gilt
isometrisch:
gilt
isometrisch:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... .34
-
Es seien
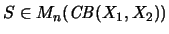 ,
,
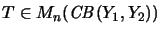 .
Für
.
Für
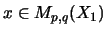 ,
,
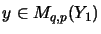 ist
ist
Nach Definition der Haagerupnorm in
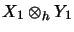 ist also
ist also
Das heißt, daß 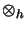 vollständig kontrahierend ist.
vollständig kontrahierend ist.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...3435
-
Die
Amplifikation
von
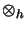 ist die
tensorielle Matrixmultiplikation
ist die
tensorielle Matrixmultiplikation
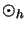 von Operatormatrizen.
von Operatormatrizen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Spurklasse-Operatoren36
- T
trägt seine natürliche Operatorraumstruktur
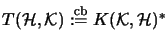 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ätze
37
- Aus der Injektivität des
Haagerup-Tensorproduktes folgen
Fortsetzungssätze
für vollständig beschränkte bilineare
(und allgemeiner multilineare) Abbildungen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kurz38
-
In der Literatur wird die Amplifikation einer bilinearen Abbildung
häufig nur für quadratische Operatormatrizen erklärt und
als die Amplifikation
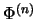 bezeichnet.
Im Lexikon benutzen wir auch die Amplifikation auf Rechteckmatrizen,
da sich dann einige
Aussagen,
in denen man bei festen
bezeichnet.
Im Lexikon benutzen wir auch die Amplifikation auf Rechteckmatrizen,
da sich dann einige
Aussagen,
in denen man bei festen
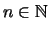 alle Amplifkationen
alle Amplifkationen
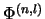 ,
,
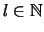 ,
verwendet, genauer beschreiben lassen.
,
verwendet, genauer beschreiben lassen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... aller39
-
Man beachte, daß die Norm der bilinearen Abbildung
im allgemeinen kleiner ist als die Norm
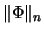 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...tex2html_comment_mark40
- Allgemeiner gilt
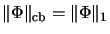 für bilineare Abbildungen in eine
kommutative C*-Algebra A,
da jede beschränkte lineare Abbildung in A automatisch vollständig beschränkt ist und
für bilineare Abbildungen in eine
kommutative C*-Algebra A,
da jede beschränkte lineare Abbildung in A automatisch vollständig beschränkt ist und
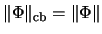 [Loe75, Lemma 1].
Für bilineare Abbildungen
[Loe75, Lemma 1].
Für bilineare Abbildungen
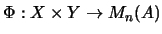 gilt
gilt
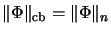 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...änkt.
41
-
Dem entspricht, daß das
Haagerup-Tensorprodukt
nicht symmetrisch ist.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ählen.
42
- Weitere Literaturangaben findet man in
[CS89, Sec. 4].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... konvergiert.43
-
Der Unterschied zur
Definition von
lokaler Reflexivität ist also, daß die
 nicht
nur kontrahierend, sondern sogar vollständig kontrahierend sein sollen.
nicht
nur kontrahierend, sondern sogar vollständig kontrahierend sein sollen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...tex2html_comment_mark44
- Für die Theorie
nuklearer C*-Algebren siehe z.B.
[Mur90] und [Pat88].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Neumann-Algebren45
- Im Zusammenhang hiermit steht das seit geraumer
Zeit offene Derivations- und äquivalent
[Kir96, Cor. 1] hierzu das
Ähnlichkeitsproblem für C*-Algebren. Man beachte, daß im Rahmen der Operatorraum-Theorie positive
Ergebnisse erzielt wurden. So zeigte
Christensen in [Chr82], daß die inneren Derivationen von
einer C*-Algebra nach
 genau die vollständig beschränkten Derivationen sind (Satz von Christensen).
genau die vollständig beschränkten Derivationen sind (Satz von Christensen).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Darstellungssatz46
- Für eine entsprechende Formulierung über die Linearisierung auf dem Haagerup-Tensorprodukt vgl.
[PS87, Thm. 2.9] !
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 setzt.47
setzt.47
- Mit der Bezeichnung
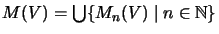 ist eine Menge K von Matrizen über V einfach
eine Teilmenge von M(V). Ihre Stufen Kn erhält man als
ist eine Menge K von Matrizen über V einfach
eine Teilmenge von M(V). Ihre Stufen Kn erhält man als
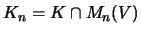 .
.
Die folgenden Definitionen lesen sich dann so:
Sei
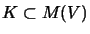 .
K heißt matrixkonvex, falls
.
K heißt matrixkonvex, falls
K heißt absolut matrixkonvex, falls
K heißt Matrixkegel, falls
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
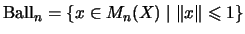 ,48
,48
-
Also
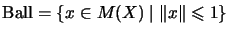 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Satz:49
-
Aus diesem Satz kann man leicht die folgende schärfere Fassung der Teile a), b) und
d) gewinnen:
- a)
- Ist K matrixkonvex, so gibt es ein
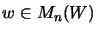 ,
,
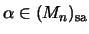 und
und
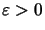 ,
so daß für alle
,
so daß für alle
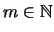 und
und 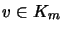
- b)
- Ist K matrixkonvex und
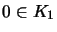 ,
so gibt es ein
,
so gibt es ein
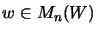 und
und
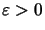 ,
so daß für alle
,
so daß für alle
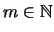 und
und 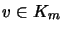
- d)
- Ist K absolut matrixkonvex, so gibt es ein
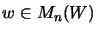 und
und
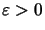 ,
so
daß für alle
,
so
daß für alle
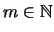 und
und 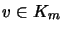
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... durch50
-
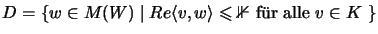
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... durch51
-
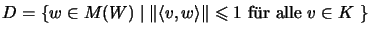
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 52
- Der Begriff ,,strukturelles Element``geht auf Morenz zurück
[Mor94]. Eine weitere äquivalente Definition wird in
[WW99] gegeben. Dort heißen die strukturellen Elemente
jedoch ,,matrix extreme points``.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...einfach53
- In [Fis96] heißen diese m-konvexen Mengen ,,endlich``.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gilt.54
- Im Fall R=Mn sind das die C*-Extremalpunkte.
Ansonsten sind R-Extremalpunkte auch C*-extremal, aber i.a. nicht umgekehrt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Nukleare55
- Die Definition der vollständig nuklearen Abbildungen
ist an den nuklearen Abbildungen der Banachraumtheorie orientiert.
Dort betrachtet man entsprechend eine Abbildung
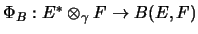 für zwei Banachräume E und F.
für zwei Banachräume E und F.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... existiert56
- In der Banachraumtheorie hat man eine analoge Aussage:
Eine Abbildung
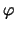 ist genau dann nuklear, wenn es ein Diagramm
ist genau dann nuklear, wenn es ein Diagramm
gibt, wobei d ein Diagonaloperator ist, d.h. es gibt ein
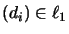 ,
so daß
,
so daß
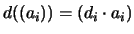 für alle
für alle
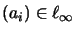 ist.
Für die nukleare Norm gilt:
ist.
Für die nukleare Norm gilt:
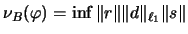 ,
wobei das Infimum über alle Faktorisierungen genommen wird.
,
wobei das Infimum über alle Faktorisierungen genommen wird.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Punkt-Norm-Topologie57
-
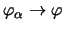 in der Punkt-Norm-Topologie, wenn
in der Punkt-Norm-Topologie, wenn
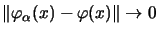 für alle
für alle 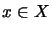 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Integrale58
- Die
integralen Abbildungen der Banachraumtheorie sind gerade der Punkt-Norm-Abschluß
der nuklearen Abbildungen. Man beachte, daß die Formeln
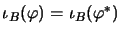 und
und
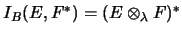 in dieser Form nur für integrale Abbildungen gelten.
in dieser Form nur für integrale Abbildungen gelten.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... identifizieren59
-
In der entstehenenden Matrix sind (i,k) die Zeilenindizes und (j,l) die
Spaltenindizes, wobei
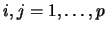 und
und
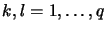 .
Die Indizes (i,k) bzw. (j,l) sind lexikographisch angeordnet.
.
Die Indizes (i,k) bzw. (j,l) sind lexikographisch angeordnet.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Rechteckmatrizen60
-
Man kann untersuchen, wie sich die shuffle-Abbildung
für Operatorraume U,V,X,Y und verschiedene
Kombinationen von Operatorraum-Tensorprodukten verhält
[EKR93, Chap. 4].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 61
- Die Dualität
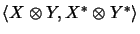 wird durch
wird durch
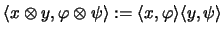 für
für
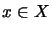 ,
,
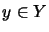 ,
,
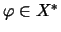 ,
,
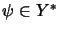 erklärt.
erklärt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...äume62
-
Seien E,F Banachräume. Dann haben wir ihre 1-direkte Summe
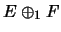 mit der Norm
mit der Norm
und ihre Summe E + F mit der Quotienten-Norm
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
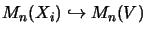 .63
.63
- Mn(V) wird mit Vn2
identifiziert.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Abbildung64
- Wir identifizieren wie
üblich
 mit seinem Dual.
mit seinem Dual.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
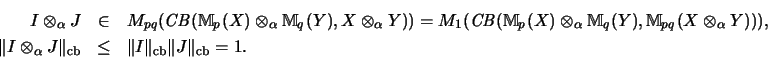
![]() (2):
Wenn
(2):
Wenn
![]() ,
,
![]() ,
,
![]() ,
so seien
,
so seien
![]() ,
,
![]() die entsprechenden Operatoren.
Nach (3) gilt
die entsprechenden Operatoren.
Nach (3) gilt
![\begin{eqnarray*}S \otimes_\alpha T
&\in&
\mathit{CB}(X_1 \otimes_\alpha Y_1, ...
...t [S_{ij}] \Vert _\mathrm{cb}\Vert [T_{kl}] \Vert _\mathrm{cb}.
\end{eqnarray*}](img380.gif)
![\begin{eqnarray*}[S_{ij} \otimes_\alpha T_{kl}]= A (S \otimes_\alpha T)
&\in& ...
...t [S_{ij}] \Vert _\mathrm{cb}\Vert [T_{kl}] \Vert _\mathrm{cb}.
\end{eqnarray*}](img382.gif)
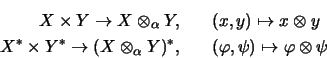
![\begin{displaymath}(\varphi \odot \psi)(x \otimes y)=
\langle x \otimes y, \var...
...times \psi_{jk} \rangle\right]
= \varphi(x)\psi(y)
\in M_n,
\end{displaymath}](img499.gif)
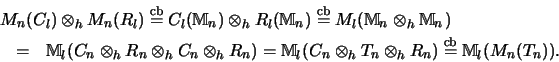
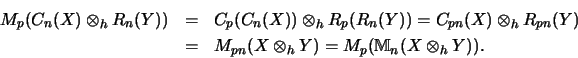
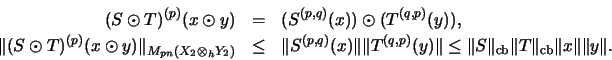
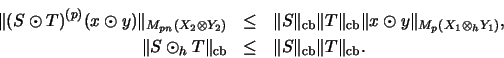
![]() .
K heißt matrixkonvex, falls
.
K heißt matrixkonvex, falls
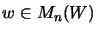 ,
,
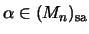 und
und
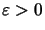 ,
so daß für alle
,
so daß für alle
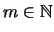 und
und 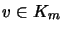
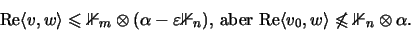
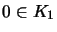 ,
so gibt es ein
,
so gibt es ein
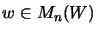 und
und
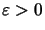 ,
so daß für alle
,
so daß für alle
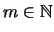 und
und 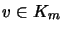
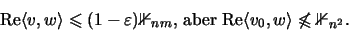
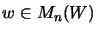 und
und
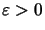 ,
so
daß für alle
,
so
daß für alle
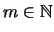 und
und