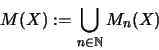Grundbegriffe

Ein  matrixnormierter Raum     ist ein Vektorraum X, versehen mit einer Norm auf jeder   Matrizenstufe   $M_n(X)=M_n\otimes X$, so daß gilt:    

(R1) $\Vert\alpha x\beta\Vert\leqslant\Vert\alpha\Vert\Vert x\Vert\Vert\beta\Vert$ für alle $x\in M_n(X)$, $\alpha\in M_{m,n}$, $\beta\in M_{n,m}$
(R2) $\Vert x\oplus y\Vert=\max\{\Vert x\Vert,\Vert y\Vert\}$ für alle $x\in M_n(X)$, $y\in M_m(X)$.¹

Eine solche Familie von Normen heißt   Operatorraumnorm. Ist für ein n (und damit für alle) M_n(X), versehen mit dieser Norm, vollständig, so heißt  X ein    Operatorraum²([Rua88], vgl. auch [Wit84a]).

Ist X ein matrixnormierter Raum (Operatorraum), so sind die Räume M_n(X)normierte Räume (Banachräume). Diese nennt man die  Stufen, genauer die Matrizenstufen von X(erste Stufe oder      Grundstufe, zweite Stufe...).³

Die Operatorraumnormen auf einem festen Vektorraum X sind durch die punktweise Ordnung auf allen Matrizenstufen geordnet. Man sagt, eine größere Operatorraumnorm    dominiere eine kleinere.

Eine lineare Abbildung $\Phi$ zwischen Operatorräumen X und Y induziert eine lineare Abbildung   $\Phi^{(n)}=\mathrm{id}_{M_n} \otimes \Phi$, genauer:

$$\begin{eqnarray*}\Phi^{(n)}:M_n(X) & \to & M_n(Y) \\ \left[x_{ij}\right] & \mapsto & \left[\Phi(x_{ij})\right] \mbox{,} \end{eqnarray*}$$

die n-te   Amplifikation von $\Phi$. $\Phi$ heißt  vollständig beschränkt,      falls

$$\Vert\Phi\Vert _{\mathrm{cb}} :=\sup\left\{\left. \Vert\Phi^{... ...t \; \right\vert \; n\in {\mathbb{N} }\right\}<\infty \mbox{,}$$

    vollständig kontrahierend, falls $\Vert\Phi\Vert _{\mathrm{cb}}\leqslant 1$ und      vollständig isometrisch, falls alle $\Phi^{(n)}$ isometrisch sind.⁴ $\Phi$ heißt     vollständige Quotientenabbildung, falls alle $\Phi^{(n)}$Quotientenabbildungen sind.⁵ Die Menge aller vollständig beschränkten Abbildungen von X nach Y bezeichnet man mit   $\mathit{CB}(X,Y)$ [Pau86, Chap. 7].

Ein Operatorraum X heißt    homogen, wenn jeder beschränkte Operator $\Phi \in B(M_1(X))$ normgleich vollständig beschränkt ist: $\Phi\in CB(X)$, und $\Vert\Phi\Vert _{\mathrm{cb}}=\Vert\Phi\Vert$ [Pis96].

Beispiele:   ${B(\mathcal{H})}$ ist ein Operatorraum durch die Identifizierung $M_n(B(\mathcal{H}))=B(\mathcal{H}^n)$. Allgemein ist jede    C^*-Algebra A ein Operatorraum, wenn man den Raum M_n(A) mit seiner eindeutigen C^*-Norm versieht. Abgeschlossene Unterräume von C^*-Algebren nennt man    konkrete Operatorräume. Jeder konkrete Operatorraum ist ein Operatorraum. Umgekehrt ist nach dem Satz von Ruan jeder Operatorraum vollständig isometrisch isomorph zu einem konkreten Operatorraum.

Kommutative C^*-Algebren   sind homogene Operatorräume.

Ist $\mathcal{H}$ ein Hilbertraum und $\Phi$ die Transposition auf ${B(\mathcal{H})}$, so ist $\Vert\Phi\Vert=1$, aber $\Vert\Phi\Vert _{\mathrm{cb}}=\dim\mathcal{H}$. Ist $\mathcal{H}$ unendlichdimensional, so ist $\Phi$ also beschränkt, aber nicht vollständig beschränkt. ${B(\mathcal{H})}$ ist für $\dim\mathcal{H}\geqslant 2$ nicht homogen [Pau86, p. 6].

Mit der Bezeichnung

$$M(X):=\bigcup_{n\in{\mathbb{N} }}M_n(X)$$

lassen sich viele Sachverhalte einfacher formulieren.⁶