




Next: Grundkonstruktionen
Up: Die kanonische Operatorraumstruktur
Previous: Die kanonische Operatorraumstruktur
Im folgenden sei
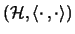 ein Hilbertraum
mit einem Skalarprodukt, das wie üblich in der ersten Komponente
linear ist.
ein Hilbertraum
mit einem Skalarprodukt, das wie üblich in der ersten Komponente
linear ist.
- 1.
-
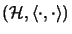 ist ein linker
Hilbert-
ist ein linker
Hilbert-
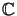 -Modul. Obige Konstruktion bietet eine Möglichkeit,
-Modul. Obige Konstruktion bietet eine Möglichkeit,
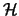 mit einer Operratorraumstruktur zu versehen. Man erhält den
Zeilen-Hilbertraum
mit einer Operratorraumstruktur zu versehen. Man erhält den
Zeilen-Hilbertraum
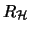 .
.
- 2.
- Um aus
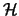 einen rechten Hilbert-
einen rechten Hilbert-
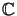 -Modul zu machen,
definiert
man auf
-Modul zu machen,
definiert
man auf
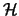 ein neues inneres Produkt durch
ein neues inneres Produkt durch
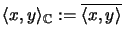 .
Der Operatorrraum, der durch obige Konstruktion entsteht, ist gerade
der
Spalten-Hilbertraum
.
Der Operatorrraum, der durch obige Konstruktion entsteht, ist gerade
der
Spalten-Hilbertraum
 .
.
- 3.
- Die Abbildung
definiert auf
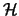 ein inneres Produkt mit Werten in
ein inneres Produkt mit Werten in
 ,
das in der ersten
Komponente linear und in der zweiten konjugiert linear ist.
Mit diesem inneren Produkt wird
,
das in der ersten
Komponente linear und in der zweiten konjugiert linear ist.
Mit diesem inneren Produkt wird
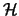 zu einem linken
Hilbert-C*-Modul über
zu einem linken
Hilbert-C*-Modul über
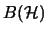 .
Der Operatorraum, der durch die obige Konstruktion
entsteht, ist gerade der
Spalten-Hilbertraum
.
Der Operatorraum, der durch die obige Konstruktion
entsteht, ist gerade der
Spalten-Hilbertraum
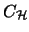 .
.
- 4.
- Die Abbildung
definiert auf
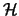 ein inneres Produkt, mit Werten in
ein inneres Produkt, mit Werten in
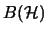 ,
das in der ersten
Komponente konjugiert linear ist und in der zweiten linear.
Mit diesem inneren Produkt und der Modulabbildung
,
das in der ersten
Komponente konjugiert linear ist und in der zweiten linear.
Mit diesem inneren Produkt und der Modulabbildung
wird
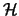 zu einem rechten
Hilbert-C*-Modul über
zu einem rechten
Hilbert-C*-Modul über
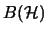 .
Der Operatorraum, der durch die obige Konstruktion
entsteht, ist gerade der
Zeilen-Hilbertraum
.
Der Operatorraum, der durch die obige Konstruktion
entsteht, ist gerade der
Zeilen-Hilbertraum
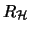 .
.
- 5.
- Die inneren Produkte aus den Beispielen im Kapitel
Rechte und linke Hilbert-C*-Moduln ,
die eine C*-Algebra A zu einem linken bzw. rechten
Hilbert-A-Modul machen, induzieren beide eine Operatorraumstruktur, die mit
der kanonischen Operatorraumstruktur von A als C*-Algebra übereinstimmt.





Next: Grundkonstruktionen
Up: Die kanonische Operatorraumstruktur
Previous: Die kanonische Operatorraumstruktur
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() ein Hilbertraum
mit einem Skalarprodukt, das wie üblich in der ersten Komponente
linear ist.
ein Hilbertraum
mit einem Skalarprodukt, das wie üblich in der ersten Komponente
linear ist.