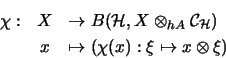Next: Abbildungsräume
Up: Hilbert-C*-Moduln
Previous: Modulabbildungen zwischen Hilbert-C*-Moduln
Jeder Hilbert-C*-Modul über einer C*-Algebra A
trägt eine kanonische Operatorraumstruktur.
Die folgenden beiden Kriterien [Ble97] erlauben, einem gegebenen
rechten Operator-A-Modul X
anzusehen, ob seine Operatorraumstruktur von einem A-wertigen
inneren Produkt
induziert wird, d.h. ob X ein rechter Hilbert-C*-Modul ist.
Die zweite Charakterisierung macht vom
Modul-Haagerup-Tensorprodukt
Gebrauch:
- a)
- Ein rechter Operator-A-Modul X ist genau dann ein
rechter Hilbert-C*-Modul über A mit seiner
kanonischen Operatorraumstruktur ,
wenn gilt:
Es gibt ein Netz positiver ganzer Zahlen
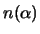 und vollständig kontrahierende A-Modulhomomorphismen
und vollständig kontrahierende A-Modulhomomorphismen
und
so daß
In diesem Fall existiert der Grenzwert
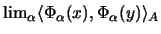 und ist gleich dem eindeutig bestimmten inneren Produkt
und ist gleich dem eindeutig bestimmten inneren Produkt
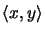 ,
das die Operatorraumstrukur induziert.
,
das die Operatorraumstrukur induziert.
- b)
- Ein rechter A-Operatormodul X ist genau dann ein rechter
Hilbert-C*-Modul über A,
wenn es eine treue, nichtentartete *-Darstellung
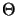 von A auf einem Hilbertraum
von A auf einem Hilbertraum
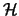 gibt, so daß gilt:
gibt, so daß gilt:
- i)
-
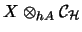 ist ein Hilbertraum.
ist ein Hilbertraum.
- ii)
- Die Abbildung
ist eine vollständige Isometrie.
- iii)
- Für alle
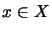 gilt
gilt
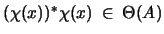 .
.
Das A-wertige innere Produkt, das die Operatorraumstruktur von X
induziert, erhält man durch die Beziehung
- iv)
-
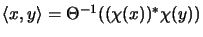 .
.
Wenn i)-iv) für eine treue, nichtentartete,
*-Darstellung erfüllt sind,
so sind sie es für jede.





Next: Abbildungsräume
Up: Hilbert-C*-Moduln
Previous: Modulabbildungen zwischen Hilbert-C*-Moduln
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
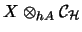 ist ein Hilbertraum.
ist ein Hilbertraum.
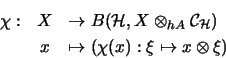
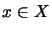 gilt
gilt
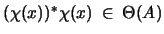 .
.
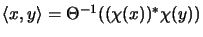 .
.