




Next: Vollständig nukleare Abbildungen
Up: Was sind Operatorräume ?
Previous: Charakterisierungen von Hilbert-C*-Moduln
Seien E, F Banachräume.
Wir betrachten einen linearen Teilraum A(E,F) des Raumes B(E,F) der stetigen Operatoren zwischen E und
F, der alle endlichrangigen Abbildungen enthält
und bezüglich einer Norm ein Banachraum ist.
Üblicherweise verlangt man noch, daß A(E,F) für alle Paare
von Banachräumen E und F erklärt ist.
Einen solchen Raum bezeichnet man nach Grothendieck als
Abbildungsraum
(Mapping space).
Analog bezeichnen wir einen Operatorraum A(X,Y), der ein linearer Teilraum von
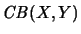 ist,
als
ist,
als
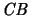 -Abbildungsraum.
Man beachte, daß i.a. die algebraische Identifizierung von
Mn(A(X,Y)) mit
A(X,Mn(Y)) nicht isometrisch ist und daß
die Normen auf
A(X,Mn(Y)) keine
Operatorraumstruktur für A(X,Y)erzeugen.
-Abbildungsraum.
Man beachte, daß i.a. die algebraische Identifizierung von
Mn(A(X,Y)) mit
A(X,Mn(Y)) nicht isometrisch ist und daß
die Normen auf
A(X,Mn(Y)) keine
Operatorraumstruktur für A(X,Y)erzeugen.
Zwischen Abbildungsräumen und Tensorprodukten besteht ein
enger Zusammenhang. So sind
der Raum F(X,Y) der
endlichrangigen Abbildungen
zwischen X und Y
und das algebraische Tensorprodukt von X* mit Y isomorph:
Diese Identifikation ermöglicht es, Normen von dem einen
Raum auf den anderen zu übertragen.
Man betrachte hierzu die Fortsetzung der Abbildung
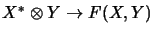 auf die Vervollständigung
auf die Vervollständigung
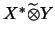 :
:
Diese muß weder injektiv noch surjektiv sein.
Als Abbildungsraum erhält man
daher
mit der
Norm von
Wir betrachten im folgenden Vorschriften, die jedem Paar von Operatorräumen einen
Abbildungsraum
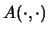 mit Operatorraumnorm
mit Operatorraumnorm
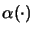 zuordnen. In der Banachraumtheorie wurde von Pietsch der Begriff des Abbildungsraumes zum Begriff
des
Operatorideals verschärft [Pie78].
Analog betrachten wir in der Operatorraumtheorie Zuordnungen,
die eine
zuordnen. In der Banachraumtheorie wurde von Pietsch der Begriff des Abbildungsraumes zum Begriff
des
Operatorideals verschärft [Pie78].
Analog betrachten wir in der Operatorraumtheorie Zuordnungen,
die eine
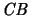 -Idealeigenschaft [ER94] haben, d.h. die Komposition
-Idealeigenschaft [ER94] haben, d.h. die Komposition
ist für alle Operatorräume X1, X2, Y1, Y2 erklärt und
allgemein vollständig kontrahierend .
Ein
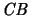 -Abbildungsraum mit der
-Abbildungsraum mit der
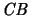 -Idealeigenschaft
heißt lokal [EJR98], wenn für seine Norm gilt:
-Idealeigenschaft
heißt lokal [EJR98], wenn für seine Norm gilt:





Next: Vollständig nukleare Abbildungen
Up: Was sind Operatorräume ?
Previous: Charakterisierungen von Hilbert-C*-Moduln
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() ist,
als
ist,
als
![]() -Abbildungsraum.
Man beachte, daß i.a. die algebraische Identifizierung von
Mn(A(X,Y)) mit
A(X,Mn(Y)) nicht isometrisch ist und daß
die Normen auf
A(X,Mn(Y)) keine
Operatorraumstruktur für A(X,Y)erzeugen.
-Abbildungsraum.
Man beachte, daß i.a. die algebraische Identifizierung von
Mn(A(X,Y)) mit
A(X,Mn(Y)) nicht isometrisch ist und daß
die Normen auf
A(X,Mn(Y)) keine
Operatorraumstruktur für A(X,Y)erzeugen.
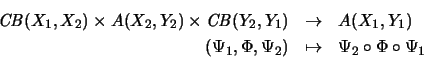
![]() -Abbildungsraum mit der
-Abbildungsraum mit der
![]() -Idealeigenschaft
heißt lokal [EJR98], wenn für seine Norm gilt:
-Idealeigenschaft
heißt lokal [EJR98], wenn für seine Norm gilt: