




Next: Symbolverzeichnis
Up: Interpolation
Previous: Schnitt und Summe
Interpolation
Seien E0, E1 Banachräume.
Das Paar (E0,E1) heißt verträglich im Sinne der
Interpolationstheorie [BL76], wenn es einen Hausdorffschen
topologischen Vektorraum V und lineare stetige Inklusionen
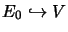 und
und
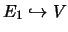 gibt.
Diese erlauben es, den
Interpolationsraum
gibt.
Diese erlauben es, den
Interpolationsraum
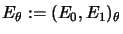 für
für
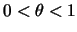 zu definieren.
Pisier führte die analoge Konstruktion für Operatorräume
ein [Pis96, §2]:
Seien Xi (i=0,1) Operatorräume. Dann haben wir spezifische
Normen auf Mn(Xi) und stetige lineare Inklusionen
zu definieren.
Pisier führte die analoge Konstruktion für Operatorräume
ein [Pis96, §2]:
Seien Xi (i=0,1) Operatorräume. Dann haben wir spezifische
Normen auf Mn(Xi) und stetige lineare Inklusionen
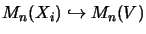 .63 Der
interpolierte Operatorraum
.63 Der
interpolierte Operatorraum 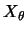 wird jetzt
über
wird jetzt
über
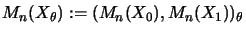 definiert.
definiert.
Seien X ein Operatorraum,
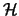 ein Hilbertraum, und es gebe eine beschränkte, lineare und injektive
Abbildung
ein Hilbertraum, und es gebe eine beschränkte, lineare und injektive
Abbildung
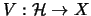 mit dichtem Bild,
so daß die Abbildung64
mit dichtem Bild,
so daß die Abbildung64
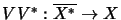 ebenfalls beschränkt, linear
und injektiv mit dichtem Bild ist.
Dann gilt vollständig isometrisch:
ebenfalls beschränkt, linear
und injektiv mit dichtem Bild ist.
Dann gilt vollständig isometrisch:
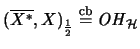 [Pis96, Cor. 2.4].
[Pis96, Cor. 2.4].
Beispiele
- 1.
-
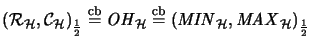
- 2.
-
Auf diese Art erhält man auch Operatorraumstrukturen auf den
Schattenidealen
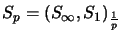 für
für
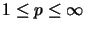 .
.
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04