



Nächste Seite: Supremum und Zwischenwertsatz
Aufwärts: Konvexe Funktionen
Vorherige Seite: Konvexe Funktionen
Inhalt
Wir zeigen, daß die Exponentialfunktion zur Basis 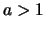 mit
rationalen Exponenten:
mit
rationalen Exponenten:
streng konvex ist.
Nach Korollar ![[*]](crossref.png) hat diese Funktion
eine eindeutige stetige Fortsetzung auf
hat diese Funktion
eine eindeutige stetige Fortsetzung auf
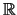 .
.
Diese Fortsetzung heißt Exponentialfunktion zur Basis 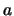 .
.
Hiermit definieren wir dann die Potenzfunktion für reelle Exponenten.
Beweis .
- Da
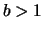 ist
ist
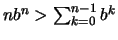 und folglich
und folglich
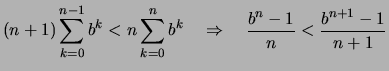 .
.
- Es seien
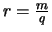 ,
,
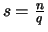 mit
mit 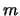 ,
, 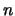 ,
,
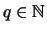 und
und
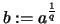 .
Es ist
.
Es ist 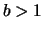 .
Aus
.
Aus 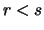 folgt
folgt 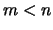 und mit (1.)
und mit (1.)
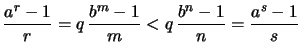 .
.
- Für
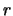 ,
, 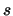 ,
,
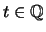 folgt aus
folgt aus 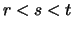 mit (2.)
mit (2.)
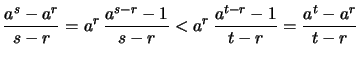 .
.
- Aus (3.) und Lemma
![[*]](crossref.png) (2.) folgt, daß die
Funktion
(2.) folgt, daß die
Funktion
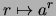 streng konvex ist.
streng konvex ist.
Es sei 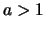 ,
,
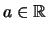 .
Nach Korollar
.
Nach Korollar ![[*]](crossref.png) hat die streng konvexe Funktion
hat die streng konvexe Funktion
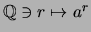 eine eindeutige stetige Fortsetzung auf
eine eindeutige stetige Fortsetzung auf
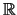 .
.
Feststellung 2.4.18 (Regeln: Exponentialfunktion)
Es sei 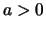 ,
,
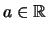 .
.
- Es gilt die Funktionalgleichung
- Es ist
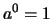 ,
,
- Für
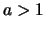 ist die Exponentialfunktion zur Basis
ist die Exponentialfunktion zur Basis 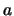 streng monoton wachsend und streng konvex.
streng monoton wachsend und streng konvex.
- Für
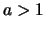 gilt
gilt
Beweis .
- Wähle Folgen
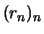 und
und 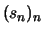 in
in
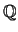 mit
mit
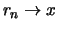 und
und 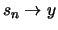 . Da die Exponetialfunktion stetig ist,
folgt:
. Da die Exponetialfunktion stetig ist,
folgt:
- Da
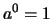 folgt
folgt
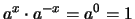 und
und
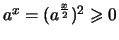 .
.
- Da die Exponentialfunktion für rationale Exponenten streng monoton ist,
folgt die strenge Monotonie der stetigen Fortsetzung wie in Beispiel
![[*]](crossref.png) .
.
Analog folgt die strenge Konvexität.
- Da
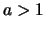 ist
ist
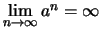 .
Da die Exponentialfunktion monoton wachsend ist, folgt hieraus
.
Da die Exponentialfunktion monoton wachsend ist, folgt hieraus
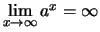 .
.
Es ist
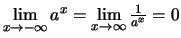 .
.
Da
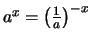 ist erhalten wir:
ist erhalten wir:
Korollar 2.4.19
Für
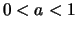
ist die Exponentialfunktion
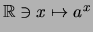
streng monoton fallend und streng konvex.
Bemerkung.
Für 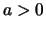 und
und
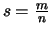 ,
,
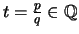 gilt
bekanntlich
gilt
bekanntlich
Beweis . Wir wählen zunächst
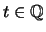 und zeigen
und zeigen
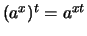 für
für
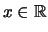 .
.
Dazu wähle man eine Folge 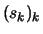 in
in
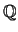 mit
mit 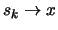 .
.
Da die Potenzfunktion
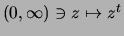 für rationale Exponenten
für rationale Exponenten 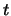 stetig ist
(vgl. Beispiel
stetig ist
(vgl. Beispiel ![[*]](crossref.png) ), erhalten wir
), erhalten wir
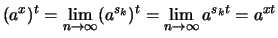 .
.
Nun wählen wir eine Folge 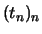 in
in
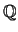 mit
mit 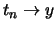 und erhalten
und erhalten
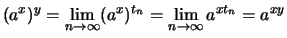 .
.
Anmerkung. Vertauschen wir die Reihenfolge der Grenzprozesse
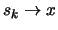 und
und 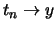 , stoßen wir auf ein Problem, da wir
noch zeigen müssen, daß die Potenzfunktion für irrationale Exponenten
stetig ist.
, stoßen wir auf ein Problem, da wir
noch zeigen müssen, daß die Potenzfunktion für irrationale Exponenten
stetig ist.
Bezeichnung 2.4.21 (Reelle Potenzen)
Für
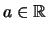 definiert man die Potenzfunktion zur Potenz
definiert man die Potenzfunktion zur Potenz 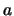 durch:
durch:
Beweis .
- Für
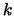 ,
,
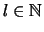 ,
, 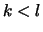 und
und 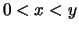 gilt
gilt
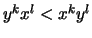 .
.
Für 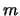 ,
,
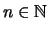 mit
mit 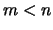 folgt daraus
folgt daraus
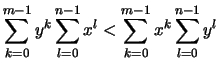 .
.
Wenn
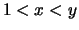 oder
oder
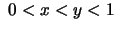 ist,
so ist
ist,
so ist
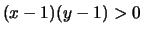 und folglich (geometrische Reihe)
und folglich (geometrische Reihe)
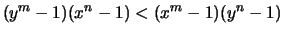 .
.
Hieraus folgt nun die Behauptung (1.).
- Es seien
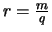 ,
,
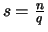 mit
mit 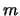 ,
, 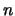 ,
,
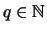 .
Da die
.
Da die 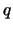 -te Wurzel streng monoton ist, gilt nach Voraussetzung
-te Wurzel streng monoton ist, gilt nach Voraussetzung
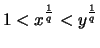 bzw.
bzw.
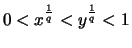 .
Aus (1.) folgt nun
.
Aus (1.) folgt nun
Die Funktion
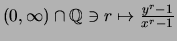 ist
streng monoton wachsend und hat eine stetige
Fortsetzung auf
ist
streng monoton wachsend und hat eine stetige
Fortsetzung auf
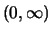 .
Nach Satz
.
Nach Satz ![[*]](crossref.png) ist die Fortsetzung streng monoton.
ist die Fortsetzung streng monoton.
Für 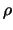 ,
,
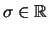 mit
mit
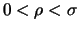 gilt also
gilt also
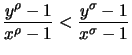 .
.
- Im Fall
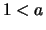 setze man in
setze man in 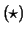
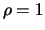 und
und 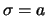 .
.
Feststellung 2.4.24 (Konvexität der Potenzfkt.)
Es sei
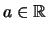 . Die Potenzfunktion
. Die Potenzfunktion
- ist streng monoton wachsend und streng konvex für
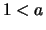 .
.
- ist streng monoton wachsend und streng konkav für
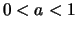 .
.
- ist streng monoton fallend und streng konvex für
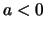 .
.
Mit der Feststellung ![[*]](crossref.png) erhält man:
erhält man:
Korollar 2.4.25
Die Potenzfunktion
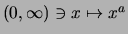 ist für jeden Exponenten
ist für jeden Exponenten
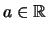 stetig.
stetig.
Auf jedem kompakten Teilintervall
![$ [c,d]\subset (0,\infty) $](img1653.png) ist die
Potenzfunktion Lipschitz-stetig.
ist die
Potenzfunktion Lipschitz-stetig.
Beweis .
- Es sei
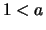 : Die die Potenzfunktion
: Die die Potenzfunktion 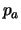 ist monoton wachsend und bijektiv,
also ist sie streng monoton wachsend.
ist monoton wachsend und bijektiv,
also ist sie streng monoton wachsend.
Für 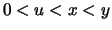 gilt nach Lemma
gilt nach Lemma ![[*]](crossref.png) (3.)
(3.)
Aus Lemma ![[*]](crossref.png) (2.) folgt nun, daß
Potenzfunktion für
(2.) folgt nun, daß
Potenzfunktion für 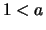 streng konvex ist.
streng konvex ist.
- Es sei
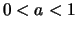 .
.
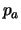 , ist die Umkehrfunktion zu
, ist die Umkehrfunktion zu
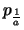 .
Nach (1.) ist
.
Nach (1.) ist
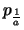 streng monoton wachsend und streng konvex.
Nach Bemerkung
streng monoton wachsend und streng konvex.
Nach Bemerkung ![[*]](crossref.png) ist die Umkehrfunktion streng monoton wachsend und streng konkav.
ist die Umkehrfunktion streng monoton wachsend und streng konkav.
- Wir untersuchen
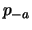 und unterscheiden drei Fälle:
und unterscheiden drei Fälle:
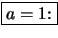
- Nach Beispiel
![[*]](crossref.png) (3.)
ist
(3.)
ist
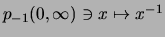 streng monoton fallend und streng konvex.
streng monoton fallend und streng konvex.
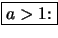
- Da
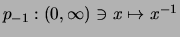 streng monoton fallend und streng konvex
ist und
streng monoton fallend und streng konvex
ist und
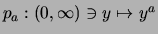 streng monoton wachsend und streng konvex ist,
ist die Komposition
streng monoton wachsend und streng konvex ist,
ist die Komposition
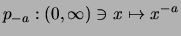 streng monton fallend und streng konvex
( vgl. Bemerkung
streng monton fallend und streng konvex
( vgl. Bemerkung ![[*]](crossref.png) (1.)).
(1.)).
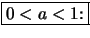
- Da
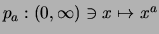 streng monoton wachsend und streng konkav ist und
streng monoton wachsend und streng konkav ist und
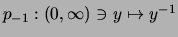 streng monoton fallend und streng konvex ist,
ist die Komposition
streng monoton fallend und streng konvex ist,
ist die Komposition
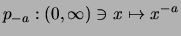 streng monoton fallend und streng konvex.
(vgl. Bemerkung
streng monoton fallend und streng konvex.
(vgl. Bemerkung ![[*]](crossref.png) (2.)).
(2.)).
Insgesamt folgt also die Behauptung (3.).




Nächste Seite: Supremum und Zwischenwertsatz
Aufwärts: Konvexe Funktionen
Vorherige Seite: Konvexe Funktionen
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() mit
rationalen Exponenten:
mit
rationalen Exponenten:
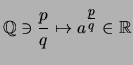
![[*]](crossref.png) hat diese Funktion
eine eindeutige stetige Fortsetzung auf
hat diese Funktion
eine eindeutige stetige Fortsetzung auf
![]() .
.
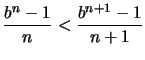 .
.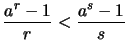 .
.
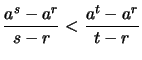 .
.
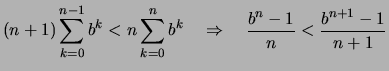 .
.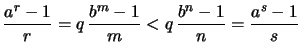 .
.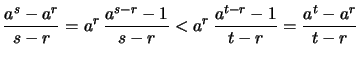 .
.![[*]](crossref.png) (2.) folgt, daß die
Funktion
(2.) folgt, daß die
Funktion
![]() ,
,
![]() .
Nach Korollar
.
Nach Korollar ![[*]](crossref.png) hat die streng konvexe Funktion
hat die streng konvexe Funktion
![]() eine eindeutige stetige Fortsetzung auf
eine eindeutige stetige Fortsetzung auf
![]() .
.
![]() ,
,
![]() .
.
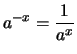 und
und ![[*]](crossref.png) .
.
![]() .
.
![]() ist erhalten wir:
ist erhalten wir:
![]() und
und
![]() ,
,
![]() gilt
bekanntlich
gilt
bekanntlich
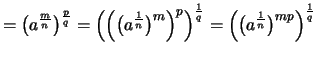
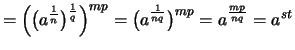 .
.![]() und zeigen
und zeigen
![]() für
für
![]() .
.
![]() in
in
![]() mit
mit ![]() .
.
![]() für rationale Exponenten
für rationale Exponenten ![]() stetig ist
(vgl. Beispiel
stetig ist
(vgl. Beispiel ![[*]](crossref.png) ), erhalten wir
), erhalten wir
![]() und
und ![]() , stoßen wir auf ein Problem, da wir
noch zeigen müssen, daß die Potenzfunktion für irrationale Exponenten
stetig ist.
, stoßen wir auf ein Problem, da wir
noch zeigen müssen, daß die Potenzfunktion für irrationale Exponenten
stetig ist.
![[*]](crossref.png) ist
ist
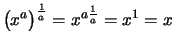 .
.![]() ,
,
![]() und
und ![]() .
.
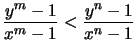 .
.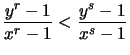 .
.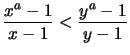 .
.![]() ,
,
![]() mit
mit ![]() folgt daraus
folgt daraus
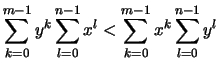 .
.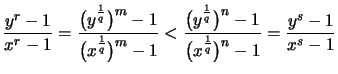
![]() ist
streng monoton wachsend und hat eine stetige
Fortsetzung auf
ist
streng monoton wachsend und hat eine stetige
Fortsetzung auf
![]() .
Nach Satz
.
Nach Satz ![[*]](crossref.png) ist die Fortsetzung streng monoton.
ist die Fortsetzung streng monoton.
![]() ,
,
![]() mit
mit
![]() gilt also
gilt also
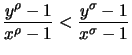 .
.![]() . Die Potenzfunktion
. Die Potenzfunktion
![[*]](crossref.png) erhält man:
erhält man:
![]() ist für jeden Exponenten
ist für jeden Exponenten
![]() stetig.
stetig.
![]() ist die
Potenzfunktion Lipschitz-stetig.
ist die
Potenzfunktion Lipschitz-stetig.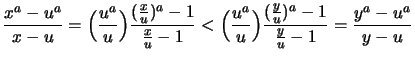
![[*]](crossref.png) (2.) folgt nun, daß
Potenzfunktion für
(2.) folgt nun, daß
Potenzfunktion für ![[*]](crossref.png) ist die Umkehrfunktion streng monoton wachsend und streng konkav.
ist die Umkehrfunktion streng monoton wachsend und streng konkav.
![[*]](crossref.png) (3.)
ist
(3.)
ist
![[*]](crossref.png) (1.)).
(1.)).
![[*]](crossref.png) (2.)).
(2.)).