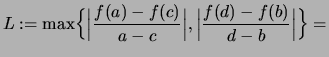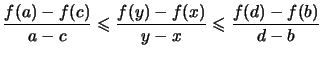Nächste Seite: Reelle Potenzen
Aufwärts: Konvexe Funktionen
Vorherige Seite: Lipschitz-stetige Funktionen
Inhalt
Bemerkung. In elementaren Büchern zum ,,Calculus ``
findet man manchmal die Veranschaulichung der stetigen Funktionen
als Funktionen, deren Graph man mit einem Stift ohne
abzusetzen zeichnen kann.
Etwas besser entsprechen die stückweise konvexen oder konkaven
Funktionen, die an den Anschlußstellen stetig zusammenpassen,
dieser Vorstellung.
Bezeichnung und Bemerkung 2.4.6 (Sekante)
- Es seien
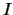 ein nichtausgeartetes Intervall und
ein nichtausgeartetes Intervall und
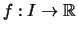 .
Für
.
Für  ,
, 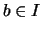 ,
, 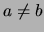 nennt man die Gerade
durch die Punkte
nennt man die Gerade
durch die Punkte 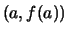 und
und 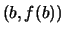 die
Sekante durch diese Punkte auf dem Graphen von
die
Sekante durch diese Punkte auf dem Graphen von 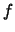 .
.
- Die Gleichung dieser Sekante lautet:
- Der Differenzenquotient
heißt die Steigung der Sekante.
Bemerkung.
Die Verbindungsstrecke der Punkte
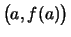 und und
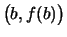 nennen wir die Sehne über dem Intervall
nennen wir die Sehne über dem Intervall ![$ [a,b] $](img882.png) . .
|
Die Sehne ist das Bild des Einheitsintervalls ![$ [0,1] $](img1485.png) unter der affinen Abbildung
unter der affinen Abbildung
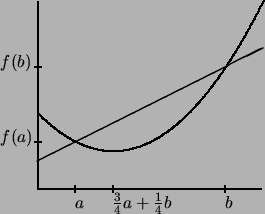
Anschaulich heißt eine Funktion konvex, wenn ihr Graph immer
unterhalb jeder Sehne verläuft.
Definition 2.4.7 (konvexe Funktion)
- Es seien
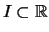 ein nichtausgeartetes Intervall.
Eine Funktion
ein nichtausgeartetes Intervall.
Eine Funktion
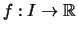 heißt konvex, wenn für alle
offenen Teilintervalle
heißt konvex, wenn für alle
offenen Teilintervalle
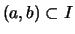 stets gilt:
stets gilt:
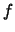 heißt streng konvex, wenn
heißt streng konvex, wenn
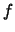 heißt konkav bzw. streng konkav, wenn
heißt konkav bzw. streng konkav, wenn 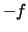 konvex bzw streng konvex ist.
konvex bzw streng konvex ist.
Durch algebraische Umformung der Definition ![[*]](crossref.png) erhält man:
erhält man:
Beweis . Es seien  ,
, 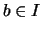 und
und 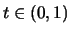 :
:
- Da
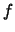 (streng) konvex und
(streng) konvex und 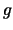 konvex und (streng ) monoton wachsend ist:
konvex und (streng ) monoton wachsend ist:
- Es ist
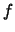 (streng) konkav:
(streng) konkav:
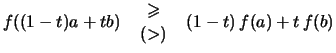 .
.
Da 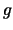 streng monoton fallend und konvex ist, folgt
streng monoton fallend und konvex ist, folgt
Beweis . Die Monotonieeigenschaften der Umkehrfunktion wurden bereits in
Satz ![[*]](crossref.png) gezeigt.
Wir zeigen jeweils den Fall strenger Konvexität bzw. strenger Konkavität.
gezeigt.
Wir zeigen jeweils den Fall strenger Konvexität bzw. strenger Konkavität.
Es seien  ,
, 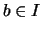 ,
,
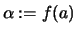 ,
,
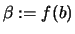 und
und 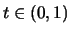 .
.
- Aus
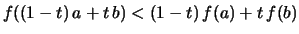 folgt
folgt
Also ist 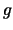 konkav.
konkav.
- Aus
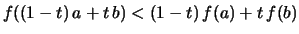 folgt
folgt
Also ist 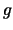 konvex.
konvex.
- Behauptung (3.) folgt analog zu (2.).
Lemma 2.4.11 (Steigung konvexer Funktionen)
Es seien
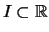
ein nichtausgeartetes Intervall
und
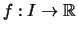
.
Die folgenden Aussagen sind äquivalent:
- Die Funktion
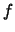 ist (streng) konvex.
ist (streng) konvex.
- Für jedes
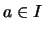 ist die Steigung
(streng) monoton wachsend.
ist die Steigung
(streng) monoton wachsend.
- Für jedes
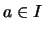 ist die Steigung
(streng) monoton wachsend.
ist die Steigung
(streng) monoton wachsend.
- Für jedes
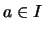 und für
und für 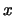 ,
, 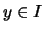 ,
, 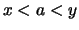 ist
ist
Korollar 2.4.12
Wenn 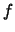 (streng) konvex ist, so ist die Steigung
(streng) konvex ist, so ist die Steigung
in beiden Variablen
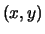
(streng) monoton wachsend.
Beweis .
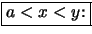
-
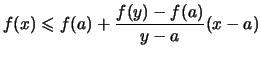
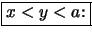
-
Analog.
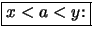
-
Da
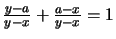 gilt:
gilt:
Beispiele 2.4.13 (Konvexität der Potenzfkt.)
- Für
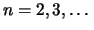 ist die Potenzfunktion
streng monoton wachsend und streng konvex:
ist die Potenzfunktion
streng monoton wachsend und streng konvex:
- Für
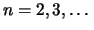 ist die Wurzelfunktion
streng monoton wachsend und streng konkav.
ist die Wurzelfunktion
streng monoton wachsend und streng konkav.
- Die Inversion
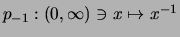 ist streng monoton
fallend und streng konvex.
ist streng monoton
fallend und streng konvex.
- Für
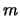 ,
,
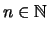 ist die Potenzfunktion
streng monoton fallend und streng konvex.
ist die Potenzfunktion
streng monoton fallend und streng konvex.
Beweis .
- Für
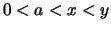 gilt für die Steigungen:
gilt für die Steigungen:
- Nach Bemerkung
![[*]](crossref.png) ist die Umkehrfunktion
streng monoton wachsend und streng konkav.
ist die Umkehrfunktion
streng monoton wachsend und streng konkav.
- Für
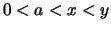 gilt für die Steigungen:
gilt für die Steigungen:
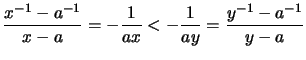 .
.
- Es seien
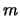 ,
,
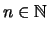 .
.
Da
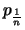 streng monoton wachsend und konkav ist und
streng monoton wachsend und konkav ist und
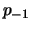 streng monoton fallend und konvex ist, ist
nach Bemerkung
streng monoton fallend und konvex ist, ist
nach Bemerkung ![[*]](crossref.png) (2.) die Komposition
(2.) die Komposition
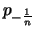 streng monoton fallend und streng konvex.
streng monoton fallend und streng konvex.
Da 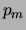 streng monoton wachsend und streng konvex ist, ist
nach Bemerkung
streng monoton wachsend und streng konvex ist, ist
nach Bemerkung ![[*]](crossref.png) (1) die Komposition
(1) die Komposition
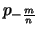 streng monoton fallend und streng konvex.
streng monoton fallend und streng konvex.
Feststellung 2.4.14 (Lipschitz-Stet. konvexer Fktn.)
Es seien
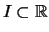 ein offenes Intervall
und
ein offenes Intervall
und
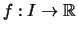 .
.
Für jedes kompakte Teilintervall
![$ J = [a,b]\subset I $](img1545.png) ist die Einschränkung
ist die Einschränkung 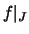 Lipschitz-stetig.
Lipschitz-stetig.
Wenn 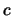 ,
,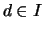 mit
mit 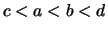 , dann ist
, dann ist
eine Lipschitz-Konstante für
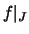
.
Beweis .
Es seien 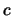 ,
,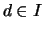 mit
mit 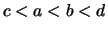 .
Nach Korollar
.
Nach Korollar ![[*]](crossref.png) gilt für
gilt für
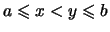
und somit
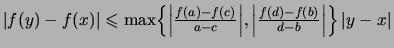 .
.
Bemerkung. Die Definition der Konvexität
![[*]](crossref.png) und die Feststellung
und die Feststellung
![[*]](crossref.png) gelten entsprechend für konvexe Funktionen
gelten entsprechend für konvexe Funktionen
 .
.
Korollar 2.4.15
Es sei
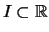
ein offenes Intervall.
Eine (streng) konvexe Funktion
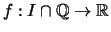
hat eine eindeutige stetige Fortsetzung
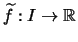
.
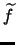
ist auch (streng) konvex.
Beweis .
Für alle
![$ J = [a,b]\subset I $](img1545.png) mit rationalen Endpunkten
mit rationalen Endpunkten
 ,
,
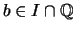 ,
, 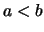 ,
ist die Einschränkung
,
ist die Einschränkung
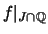 Lipschitz-stetig und hat
nach Satz
Lipschitz-stetig und hat
nach Satz ![[*]](crossref.png) eine eindeutige stetige
Fortsetzung auf
eine eindeutige stetige
Fortsetzung auf ![$ [a,b] $](img882.png) .
.
Wenn zwei derartige Intervalle ![$ [a_1,b_1] $](img1556.png) und
und ![$ [a_2,b_2] $](img1557.png) einen
nichtleeren Durchschnitt haben,
so ist der Durchschnitt ein rationaler Punkt oder ein
nichtausgeartetes Intervall mit rationalen Endpunkten.
einen
nichtleeren Durchschnitt haben,
so ist der Durchschnitt ein rationaler Punkt oder ein
nichtausgeartetes Intervall mit rationalen Endpunkten.
In beiden Fällen stimmen die jeweiligen Fortsetzungen
auf dem Durchschnitt überein.
Nach Bemerkung
![[*]](crossref.png) gibt es zu
gibt es zu 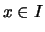 rationale
rationale  ,
,
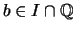 mit
mit 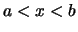 .
.
Also hat 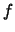 eine eindeutige stetige Fortsetzung
eine eindeutige stetige Fortsetzung
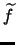 auf ganz
auf ganz 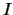 .
.
Nach Lemma ![[*]](crossref.png) und Beispiel
und Beispiel ![[*]](crossref.png) ist
ist
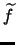 ist wieder (streng) konvex.
ist wieder (streng) konvex.




Nächste Seite: Reelle Potenzen
Aufwärts: Konvexe Funktionen
Vorherige Seite: Lipschitz-stetige Funktionen
Inhalt
Analysis1-A.Lambert
2001-02-09
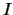 ein nichtausgeartetes Intervall und
ein nichtausgeartetes Intervall und
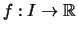 .
Für
.
Für  ,
, 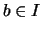 ,
, 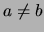 nennt man die Gerade
durch die Punkte
nennt man die Gerade
durch die Punkte 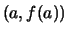 und
und 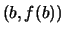 die
Sekante durch diese Punkte auf dem Graphen von
die
Sekante durch diese Punkte auf dem Graphen von 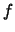 .
.
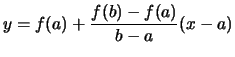 für
für  .
.
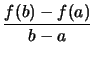
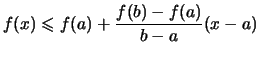 für
für
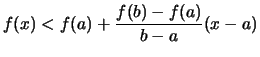 für
für
![[*]](crossref.png)
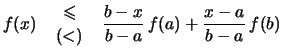 .
.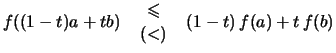 .
.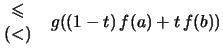
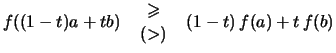 .
.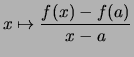 für
für 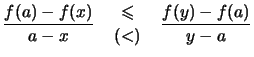
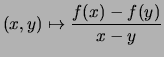 für
für 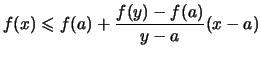
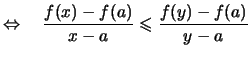
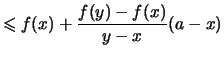
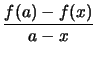
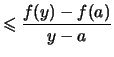 .
.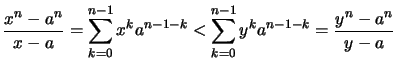
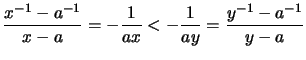 .
.