Es seien
![]() eine Folge und
eine Folge und
![]() eine
streng monoton wachsende Folge in
eine
streng monoton wachsende Folge in
![]() .
Die durch
.
Die durch
Es seien
![]() eine Folge und
eine Folge und
![]() eine
streng monoton wachsende Folge in
eine
streng monoton wachsende Folge in
![]() .
Die durch
.
Die durch
Bemerkung Der Begriff Teilfolge ist ein Spezialfall des Begriffs Komposition von Funktionen:
Nach Definition ![[*]](crossref.png) ist eine Folge eine Abbildung
ist eine Folge eine Abbildung
![]() .
Ist
.
Ist
![]() strikt monoton wachsend,
dann heißt die Komposition
strikt monoton wachsend,
dann heißt die Komposition
![]() eine Teilfolge der Folge
eine Teilfolge der Folge ![]() .
.
Man schreibt kurz
![]() und
und
![]() .
.
Als Spezialfall von Satz ![[*]](crossref.png) erhalten wir
unmittelbar:
erhalten wir
unmittelbar:
Jede Teilfolge einer konvergenten Folge ist konvergent und hat den gleichen Grenzwert.
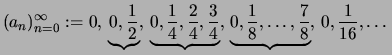
Beweis . Für
![]() setze man:
setze man:
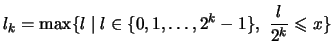 ,
,
Jede beschränkte Folge reeller Zahlen hat eine konvergente Teilfolge.
BOLZANO, Bernard, (1781-1848), Buch: Paradoxien des Unendlichen (1851).
WEIERSTRASS, Karl (1815-1897).
Zum Beweis zeigen wir ein Lemma:
Jede Folge in
![]() hat eine monotone Teilfolge.
hat eine monotone Teilfolge.
Beweis des Lemmas. Für diesen Beweis verwenden wir die folgende Bezeichnung:
Eine
![]() heiße eine Spitze der Folge
heiße eine Spitze der Folge ![]() , wenn
für alle
, wenn
für alle ![]() das Glied
das Glied ![]() ist.
ist.
Wir unterscheiden zwei Fälle:
![[*]](crossref.png) )
)
![[*]](crossref.png) )
)
Beweis (Satz von Bolzano-Weierstraß).
Da nach Satz ![[*]](crossref.png) jede beschränkte monotone Folge in
jede beschränkte monotone Folge in
![]() konvergent ist,
folgt der Satz unmittelbar aus Lemma
konvergent ist,
folgt der Satz unmittelbar aus Lemma ![[*]](crossref.png) .
.
Man kann die großen Sätze
des Abschnittes ![[*]](crossref.png) über stetige Funktionen auf kompakten Intervallen
auch mit Hilfe des Satzes von Bolzano-Weierstraß
beweisen.
über stetige Funktionen auf kompakten Intervallen
auch mit Hilfe des Satzes von Bolzano-Weierstraß
beweisen.
![[*]](crossref.png) (Satz von der gleichmäßigen Stetigkeit) vor:
(Satz von der gleichmäßigen Stetigkeit) vor:
Beweis (Satz von der gleichmäßigen Stetigkeit).
Wenn
![]() nicht gleichmäßig stetig ist, gibt es ein
nicht gleichmäßig stetig ist, gibt es ein
![]() und Folgen
und Folgen ![]() ,
, ![]() in
in ![]() so, daß
so, daß
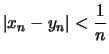 und
und
Da ![]() stetig ist, folgt ein Widerspruch:
stetig ist, folgt ein Widerspruch: