



Nächste Seite: Partielle Integration
Aufwärts: Integral von Regelfunktionen (Entwurf
Vorherige Seite: Logarithmus als Stammfunktion
Inhalt
Bemerkung. Die Riemannschen Summen
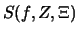 approximieren auch das Integral einer Regelfunktion
approximieren auch das Integral einer Regelfunktion 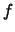 .
.
Die Riemannschen Summen von Regelfunktionen
werden vorwiegend dazu verwendet,
gewisse Eigenschaften endlicher Summen auf Integrale
zu übertragen.
Lemma 3.1.30
Es sei
![$ t:[a,b]\rightarrow \mathbb{R}$](img2210.png)
eine Treppenfunktion.
Dann gibt es zu jedem
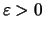
ein
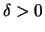
, so daß
für jede Zerlegung
von
![$ [a,b] $](img882.png)
der Feinheit
und jede Wahl von Stützstellen
die Riemannsche Summe
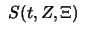
das Integral mit einem
Fehler, der kleiner als
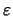
ist, approximiert:
![$\displaystyle \textstyle
\bigl\vert\; S(t,Z,\Xi)\ -\int\limits_{[a,b]}\!t\ \bigr\vert < \varepsilon$](img2396.png) .
.
Beweis . Zu der Treppenfunktion 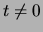 gibt es eine Zerlegung
gibt es eine Zerlegung
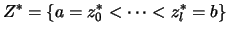 ,
,
so daß
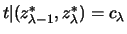 konstant ist.
Man setze
konstant ist.
Man setze
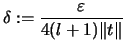 .
.
Es sei nun
eine Zerlegung.
Durch Induktion über die Anzahl 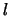 der Teilpunkte zeigt man:
Es gibt höchstens
der Teilpunkte zeigt man:
Es gibt höchstens 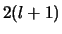 abgeschlossene Teilintervalle
abgeschlossene Teilintervalle
![$ [x_{\varkappa-1},x_\varkappa] $](img2312.png) , die einen der Punkte
, die einen der Punkte
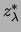 enthalten. Es sei
enthalten. Es sei
![$\displaystyle M :=\{ \varkappa \mid \varkappa\in\{1,\dots,k\},\
\exists\; z_\lambda^*\in [x_{\varkappa-1},x_\varkappa]\, \}$](img2404.png) .
.
und
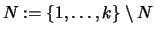 .
.
Wenn die Feinheit
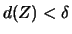 , dann folgt für jede
zulässige Wahl von Stützstellen
, dann folgt für jede
zulässige Wahl von Stützstellen
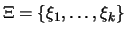 :
:
Man beachte, daß die Summanden für
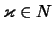 verschwinden, da
verschwinden, da
![$ f\big\vert[x_{\varkappa-1},x_\varkappa] $](img2412.png) konstant ist.
Folglich gilt
konstant ist.
Folglich gilt
Satz 3.1.31 (Aproximation durch Riemann-Summen)
Es sei
![$ f\in \mathcal{R}([a,b]) $](img2197.png)
.
Dann gibt es zu jedem
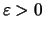
ein
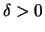
, so daß
für jede Zerlegung
von
![$ [a,b] $](img882.png)
der Feinheit
und jede Wahl von Stützstellen
die Riemannsche Summe
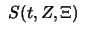
das Integral mit einem
Fehler, der kleiner als
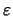
ist, approximiert:
![$\displaystyle \textstyle
\bigl\vert\; S(f,Z,\Xi)\ -\int\limits_{[a,b]}\!f \bigr\vert < \varepsilon$](img2414.png) .
.
Beweis . Zu der Regelfunktion
![$ f\in \mathcal{R}([a,b]) $](img2197.png) gibt es eine
Treppenfunktion
gibt es eine
Treppenfunktion 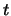 , so daß auf
, so daß auf ![$ [a,b] $](img882.png) gilt:
gilt:
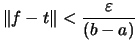 .
.
Zu 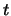 gibt es nach Lemma
gibt es nach Lemma ![[*]](crossref.png) ein
ein 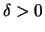 , so daß
für jede Zerlegung
, so daß
für jede Zerlegung 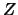 der Feinheit
der Feinheit
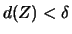 und jede zulässige Wahl von Stützstellen
und jede zulässige Wahl von Stützstellen  stets
stets
![$\displaystyle \textstyle
\bigl\vert\; S(t,Z,\Xi)\ -\int\limits_{[a,b]}\!t\ \bigr\vert < \varepsilon$](img2396.png) .
.
ist. Dann folgt
Korollar 3.1.32 (Konvergenz der Riemann-Summen)
Es sei
![$ f\in \mathcal{R}([a,b]) $](img2197.png)
.
Für jede Folge
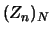
von Zerlegungen des Intervalls
![$ [a,b] $](img882.png)
, deren Feinheit gegen Null strebt:
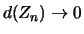 ,
,
und jede zulässige Wahl von Stützpunkten
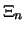
,
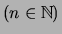
,
konvergieren die Riemannschen Summen gegen das Integral von
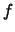
:
Bemerkung
Dagegen approximieren die entsprechenden Treppenfunktionen
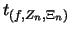 (Def.
(Def. ![[*]](crossref.png) )
im allgemeinen die Funktion
)
im allgemeinen die Funktion 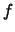 nicht gleichmäßig. In der
nicht gleichmäßig. In der 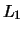 -Norm
gilt aber:
-Norm
gilt aber:
![$\displaystyle \textstyle
\lim\limits_{n\to\infty} \Vert f-t_n \Vert _1 :=
\lim\limits_{n\to\infty} \int\limits_{[a,b]} \vert f-t_n\vert = 0$](img2422.png) .
.
Konvergenz in der 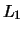 -Norm untersuchen wir in Analysis III.
-Norm untersuchen wir in Analysis III.




Nächste Seite: Partielle Integration
Aufwärts: Integral von Regelfunktionen (Entwurf
Vorherige Seite: Logarithmus als Stammfunktion
Inhalt
Analysis1-A.Lambert
2001-02-09
![]() approximieren auch das Integral einer Regelfunktion
approximieren auch das Integral einer Regelfunktion ![]() .
.
![$\displaystyle \textstyle
\bigl\vert\; S(t,Z,\Xi)\ -\int\limits_{[a,b]}\!t\ \bigr\vert < \varepsilon$](img2396.png) .
.![]() gibt es eine Zerlegung
gibt es eine Zerlegung
![]() , dann folgt für jede
zulässige Wahl von Stützstellen
, dann folgt für jede
zulässige Wahl von Stützstellen
![]() :
:
![$\displaystyle = \sum_{\varkappa\in M} \Bigl( f(\xi_\varkappa)(x_\varkappa\!-\!x...
... -\!\!{\textstyle \int\limits_{[x_{\varkappa-1},x_\varkappa]}\!\!\!\!t}\ \Bigr)$](img2408.png)
![$\displaystyle \qquad + \sum_{\varkappa\in N} \Bigl( f(\xi_\varkappa)(x_\varkapp...
...-\!\! {\textstyle\int\limits_{[x_{\varkappa-1},x_\varkappa]}\!\!\!\!t\ } \Bigr)$](img2409.png)
![$\displaystyle = \sum_{\varkappa\in M} \Bigl( f(\xi_\varkappa)(x_\varkappa\!-\!x...
...)\ -\!\! {\textstyle\int\limits_{[x_{\varkappa-1},x_\varkappa]}\!\!\!t}\ \Bigr)$](img2410.png)
![$\displaystyle \bigl\vert\, S(t,Z,\Xi)\ -{\textstyle\int\limits_{[a,b]}\!t} \,\bigr\vert
\ <\ 2\,(l+1)\, 2\,\Vert t\Vert\, \delta = \varepsilon .
$](img2413.png)
![$\displaystyle \textstyle
\bigl\vert\; S(f,Z,\Xi)\ -\int\limits_{[a,b]}\!f \bigr\vert < \varepsilon$](img2414.png) .
.![]() gibt es eine
Treppenfunktion
gibt es eine
Treppenfunktion ![]() , so daß auf
, so daß auf ![]() gilt:
gilt:
![[*]](crossref.png) ein
ein ![$\displaystyle \textstyle
\bigl\vert\; S(t,Z,\Xi)\ -\int\limits_{[a,b]}\!t\ \bigr\vert < \varepsilon$](img2396.png) .
.![$\displaystyle \textstyle\ - \int\limits_{[a,b]}\!f \,\bigr\vert$](img2417.png)
![$\displaystyle \textstyle\strut\qquad + \bigl\vert\, S(t,Z,\Xi)\ -\int\limits_{[...
...bigr\vert + \bigl\vert\, \int\limits_{[a,b]}\!(t-f) \,\bigr\vert < 3\varepsilon$](img2419.png) .
.![$\displaystyle \textstyle
\lim\limits_{n\to\infty}S(f,Z_n,\Xi_n)
= \int\limits_{[a,b]}f
$](img2328.png)
![]() (Def.
(Def. ![[*]](crossref.png) )
im allgemeinen die Funktion
)
im allgemeinen die Funktion ![]() nicht gleichmäßig. In der
nicht gleichmäßig. In der ![]() -Norm
gilt aber:
-Norm
gilt aber:
![$\displaystyle \textstyle
\lim\limits_{n\to\infty} \Vert f-t_n \Vert _1 :=
\lim\limits_{n\to\infty} \int\limits_{[a,b]} \vert f-t_n\vert = 0$](img2422.png) .
.