



Nächste Seite: Riemannsche Summen von Regelfunktionen
Aufwärts: Integral von Regelfunktionen (Entwurf
Vorherige Seite: Integration stetiger Funktionen
Inhalt
Bemerkung.
Wir untersuchen die Stammfunktion
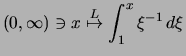 .
.
und zeigen, daß
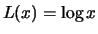 der natürliche Logarithmus ist.
der natürliche Logarithmus ist.
Die Bezeichnung 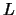 verwenden wir nur im Beweis des folgenden
Satzes.
verwenden wir nur im Beweis des folgenden
Satzes.
Zur Identifizierung 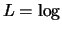 benötigen wir eine Charakterisierung
der Exponentialfunktion.
benötigen wir eine Charakterisierung
der Exponentialfunktion.
Bemerkung 3.1.28 (Funktionalgleichung)
Es sei
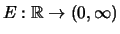 stetig und es gelte
stetig und es gelte
und
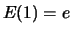
. Dann gilt
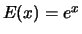
für
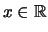
.
Beweis . Induktiv folgt
Weiterhin folgt aus der Funktionalgleichung
Aus der Eindeutigkeit der 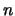 -ten Wurzel folgt
Da
-ten Wurzel folgt
Da 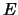 stetig ist, folgt mit
stetig ist, folgt mit ![[*]](crossref.png) , daß
, daß
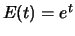 für
für
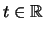 .
.
Beweis . Wir bezeichnen das Integral mit
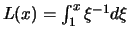 .
.
- es ist
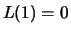 .
Da der Integrand streng positiv ist, ist
.
Da der Integrand streng positiv ist, ist 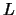 streng monoton
wachsend.
streng monoton
wachsend.
- Nach der Transformationsformel
![[*]](crossref.png) gilt mit der affinen Transformation
gilt mit der affinen Transformation
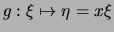 ,
, 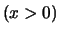 :
Hiermit folgt:
:
Hiermit folgt:
- Für
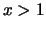 gilt
gilt
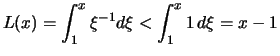 .
.
Für 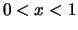 gilt
gilt
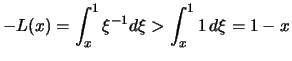 .
.
Also gilt
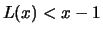 für
für
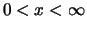 ,
, 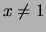 .
.
Dann folgt
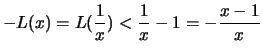 .
.
- Da die Stammfunktion
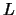 stetig ist, folgt aus (3.)
stetig ist, folgt aus (3.)
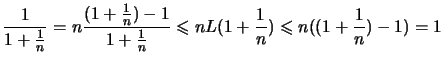 .
.
Also ist
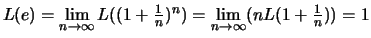 .
.
- Da
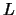 monoton wachsend ist, gilt
monoton wachsend ist, gilt
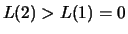 und
und analog
und
und analog
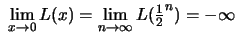 .
.
also ist das Bild
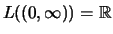 .
.
- Es gibt die stetige, streng monoton wachsende Umkehrfunktion
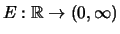 von
von 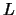 .
.
Aus (4.) folgt 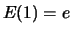 und aus (2.) folgt
und aus (2.) folgt
Also gilt nach Bemerkung ![[*]](crossref.png)
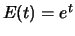 für
für
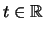 und somit nach Definition
und somit nach Definition ![[*]](crossref.png)
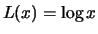 für
für
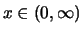 .
.




Nächste Seite: Riemannsche Summen von Regelfunktionen
Aufwärts: Integral von Regelfunktionen (Entwurf
Vorherige Seite: Integration stetiger Funktionen
Inhalt
Analysis1-A.Lambert
2001-02-09
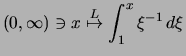 .
.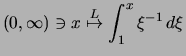 .
.![]() verwenden wir nur im Beweis des folgenden
Satzes.
verwenden wir nur im Beweis des folgenden
Satzes.
![]() benötigen wir eine Charakterisierung
der Exponentialfunktion.
benötigen wir eine Charakterisierung
der Exponentialfunktion.
![[*]](crossref.png) , daß
, daß
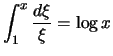 .
.![]() .
.
![[*]](crossref.png) gilt mit der affinen Transformation
gilt mit der affinen Transformation
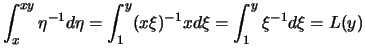
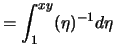
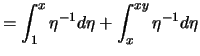
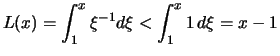 .
.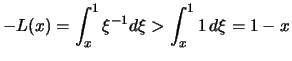 .
.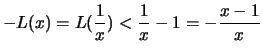 .
.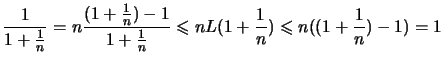 .
.![]() .
.
![]() und aus (2.) folgt
und aus (2.) folgt
![[*]](crossref.png)
![[*]](crossref.png)