



Nächste Seite: Logarithmus als Stammfunktion
Aufwärts: Integral von Regelfunktionen (Entwurf
Vorherige Seite: Integral von Regelfunktionen
Inhalt
Bemerkung.
Wir bringen hier nur ganz wenige Beispiele
von Integralen elementarer Funktionen.
Leichter berechnet man diese Integrale später mit
den folgenden Hilfmitteln:
- Hauptsatz der Differential- und Integralrechnung.
- Partielle Integration
![[*]](crossref.png)
- Substitution
![[*]](crossref.png)
- Integration der Umkehrfunktion
![[*]](crossref.png)
Bemerkung. Die zu berechnende Fläche ist ein
gleichschenkliges, rechtwinkliges Dreieck mit Katheten
der Länge 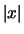 . Aus der Geometrie weiß man, daß
die Dreiecksfläche
. Aus der Geometrie weiß man, daß
die Dreiecksfläche
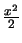 ist.
ist.
Beweis . Wähle die äquidistante Zerlegung des Intervalls ![$ [0,x] $](img2299.png) in
in 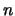 Teile,
Teile,
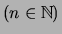 :
:
und approximiere die Funktion
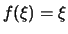 durch
die Treppenfunktion
Die Folge
durch
die Treppenfunktion
Die Folge 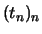 konvergiert gleichmäßig gegen
konvergiert gleichmäßig gegen 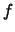 und somit gilt:
und somit gilt:
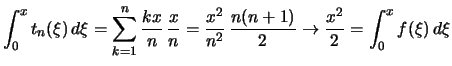 .
.
Bemerkung. Für eine stetige Funktion kann man leicht
approximierende Treppenfunktionen angeben:
Bezeichnung 3.1.22
Es sei
![$ f: [a,b] \rightarrow \mathbb{R}$](img1742.png) stetig.
Zu einer Zerlegung des Intervalls
stetig.
Zu einer Zerlegung des Intervalls ![$ [a,b] $](img882.png)
und einer Menge

von
Stützstellen
bildet man die Treppenfunktion
Bezeichnung 3.1.23 (Feinheit einer Zerlegung)
Wenn
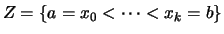 eine Zerlegung ist,
so heißt heißt das Maximum der Längen der Teilintervalle
eine Zerlegung ist,
so heißt heißt das Maximum der Längen der Teilintervalle
![$ [x_{\varkappa-1},x_\varkappa] $](img2312.png) die Feinheit der Zerlegung.
Die Feinheit wird mit
die Feinheit der Zerlegung.
Die Feinheit wird mit
bezeichnet.
Bemerkung. Wenn
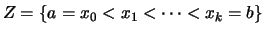 eine Zerlegung ist, so nennen wir eine Menge von Stützstellen
eine Zerlegung ist, so nennen wir eine Menge von Stützstellen
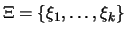 zulässig, wenn
zulässig, wenn
![$ \xi_\varkappa\in[x_{\varkappa-1},x_\varkappa] $](img2316.png) für
für
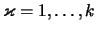 ist.
ist.
Satz 3.1.24 (Approximierende Treppenunktion)
Es sei
![$ f: [a,b] \rightarrow \mathbb{R}$](img1742.png) stetig.
Dann gibt es zu jedem
stetig.
Dann gibt es zu jedem
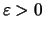 ein
ein 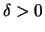 , so daß
für jede Zerlegung
, so daß
für jede Zerlegung 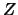 von
von ![$ [a,b] $](img882.png) der Feinheit
der Feinheit
und jede zulässige Wahl von Stützstellen

der Abstand von
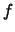
zu der Treppenfunktion
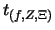
kleiner als
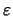
ist:
Beweis . Nach Satz ![[*]](crossref.png) ist
ist 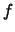 gleichmäßig stetig:
gleichmäßig stetig:
![$\displaystyle \forall \varepsilon >0 \,\exists\; \delta>0 \,\forall x,y\in [a,b]\
:\ \vert x-y\vert<\delta \Rightarrow \vert f(x)-f(y)\vert<\varepsilon$](img2321.png) .
.
Für eine Zerlegung 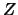 mit
mit
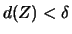 und jede
zulässige Menge von Stützpunkten gilt dann
und somit
und jede
zulässige Menge von Stützpunkten gilt dann
und somit
Bezeichnung 3.1.25
Es sei
![$ f: [a,b] \rightarrow \mathbb{R}$](img1742.png)
eine Funktion. Zu einer
Zerlegung des Intervalls
![$ [a,b] $](img882.png)
und einer Menge

von zulässigen
Stützstellen
bildet man die
Riemansche Summe:
BERNHARDT RIEMANN, 1826-1866
Bemerkung.
Eine Riemannsche Summe ist eine endliche Summe, zu deren
Berechnung man nur endlich viele Funktionswerte des
Integranden brauch.
Satz 3.1.26 (Konvergenz der Riemann-Summen)
Es sei
![$ f: [a,b] \rightarrow \mathbb{R}$](img1742.png) stetig..
Für jede Folge
stetig..
Für jede Folge 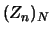 von Zerlegungen des Intervalls
von Zerlegungen des Intervalls
![$ [a,b] $](img882.png) , deren Feinheit gegen Null strebt:
, deren Feinheit gegen Null strebt:
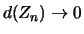 ,
,
und jede zulässige Wahl von Stützpunkten
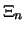
,
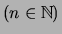
,
konvergieren die
Riemanschen Summen:
gegen das Integral von
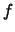
:
Beispiele 3.1.27
- Man wähle die äquidistante Zerlegung des Intervalls
![$ [0,x] $](img2299.png) in
in 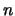 Teile:
und zeige
Teile:
und zeige
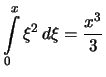 .
.
- Man wähle die Einteilung von
![$ [1,x] $](img2330.png) mit geometrischer Progression
mit geometrischer Progression
![$ q :=\sqrt[n]{\strut x} $](img2331.png) :
und zeige
:
und zeige
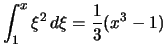 .
.
- Mit Hilfe der obigen Einteilung mit geometrischer Progression
zeige man
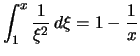 .
.
Beweis . 1. Wählt man die äquidistante Zerlegung des Intervalls ![$ [0,x] $](img2299.png) in
in 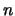 Teile,
Teile,
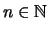 ,
und
,
und
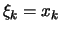 so lauten die Riemann-Summen:
so lauten die Riemann-Summen:
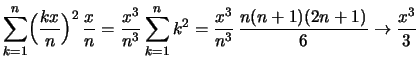 .
.
2. Wählt man eine Einteilung von ![$ [1,x] $](img2330.png) mit geometrischer Progression
mit geometrischer Progression
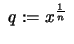 so erhält man die Teil- und Stützpunkte
und die Riemann-Summen
so erhält man die Teil- und Stützpunkte
und die Riemann-Summen
3. Für die Teil- und Stützpunkte
erhält man die Riemann-Summen




Nächste Seite: Logarithmus als Stammfunktion
Aufwärts: Integral von Regelfunktionen (Entwurf
Vorherige Seite: Integral von Regelfunktionen
Inhalt
Analysis1-A.Lambert
2001-02-09
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
![[*]](crossref.png)
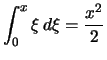 für
für
![]() . Aus der Geometrie weiß man, daß
die Dreiecksfläche
. Aus der Geometrie weiß man, daß
die Dreiecksfläche
![]() ist.
ist.
![]() in
in ![]() Teile,
Teile,
![]() :
:
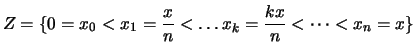
![$\displaystyle t_n : \xi \mapsto \left\{\begin{array}{ll}
\frac{kx}{n}
&\text{f\...
...,\frac{kx}{n}] \),}
\\
0 &\text{f\uml ur \( \xi = 0 \).}
\end{array}\right.
$](img2303.png)
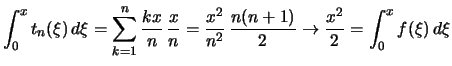 .
.![]() stetig.
Zu einer Zerlegung des Intervalls
stetig.
Zu einer Zerlegung des Intervalls ![]()
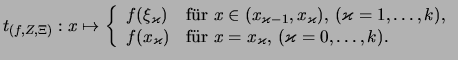
![]() eine Zerlegung ist,
so heißt heißt das Maximum der Längen der Teilintervalle
eine Zerlegung ist,
so heißt heißt das Maximum der Längen der Teilintervalle
![]() die Feinheit der Zerlegung.
Die Feinheit wird mit
die Feinheit der Zerlegung.
Die Feinheit wird mit
![]() eine Zerlegung ist, so nennen wir eine Menge von Stützstellen
eine Zerlegung ist, so nennen wir eine Menge von Stützstellen
![]() zulässig, wenn
zulässig, wenn
![]() für
für
![]() ist.
ist.
![]() stetig.
Dann gibt es zu jedem
stetig.
Dann gibt es zu jedem
![]() ein
ein ![]() , so daß
für jede Zerlegung
, so daß
für jede Zerlegung ![]() von
von ![]() der Feinheit
der Feinheit
![[*]](crossref.png) ist
ist ![]() gleichmäßig stetig:
gleichmäßig stetig:
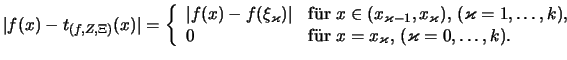
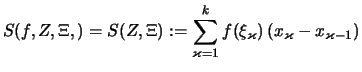
![]() stetig..
Für jede Folge
stetig..
Für jede Folge ![]() von Zerlegungen des Intervalls
von Zerlegungen des Intervalls
![]() , deren Feinheit gegen Null strebt:
, deren Feinheit gegen Null strebt:
![$\displaystyle \textstyle
\lim\limits_{n\to\infty}S(f,Z_n,\Xi_n)
= \int\limits_{[a,b]}f
$](img2328.png)
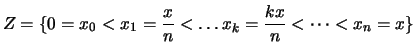
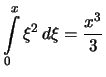 .
.
![$ q :=\sqrt[n]{\strut x} $](img2331.png) :
:
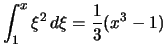 .
.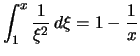 .
.![]() in
in ![]() Teile,
Teile,
![]() ,
und
,
und
![]() so lauten die Riemann-Summen:
so lauten die Riemann-Summen:
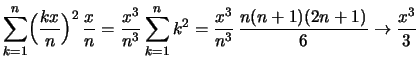 .
.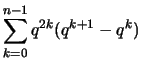
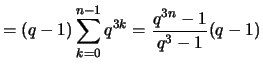
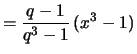
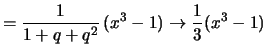 .
.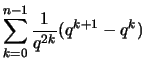
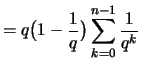
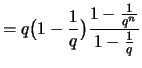
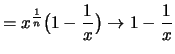 .
.