![[*]](crossref.png) für affine, monoton wachsende Transformationen
verallgemeinern.
für affine, monoton wachsende Transformationen
verallgemeinern.
Bemerkung.
Wir wollen die Transformationsformel ![[*]](crossref.png) für affine, monoton wachsende Transformationen
verallgemeinern.
für affine, monoton wachsende Transformationen
verallgemeinern.
Eine affine Funktion ![]() ist die Stammfunktion einer
konstanten Funktion
ist die Stammfunktion einer
konstanten Funktion
![]() :
:
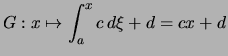 .
.![[*]](crossref.png) für affine, monoton wachsende Transformationen
für affine, monoton wachsende Transformationen
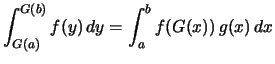 .
.
Gegeben sei eine Funktionenfolge
![]() in
in
![]() ,
die gleichmäßig auf
,
die gleichmäßig auf ![]() gegen eine Grenzfunktion
gegen eine Grenzfunktion
![]() konvergiert.
konvergiert.
Für jede stetige Funktion
![]() gilt dann:
gilt dann:
Die folgende Transformationsformel gilt
auch ohne die Voraussetzung
![]() .
Wir werden dies im nächsten Kapitel als Folgerung der
Kettenregel zeigen.
.
Wir werden dies im nächsten Kapitel als Folgerung der
Kettenregel zeigen.
Es sei
![]() ,
,
![]() , und
, und
![]() ein unbestimmtes Integral von
ein unbestimmtes Integral von ![]() .
Also ist
.
Also ist ![]() eine stetige, monoton wachsende Abbildung
von
eine stetige, monoton wachsende Abbildung
von ![]() auf
auf
![]() .
.
Für jede stetige Funktion
![]() gilt die Transformationsformel
gilt die Transformationsformel
![$\displaystyle \int\limits_{[G(a),G(b)]} \!\!\!\!\! f =
\int\limits_{[a,b]} (f\circ G) \cdot g$](img2587.png) .
.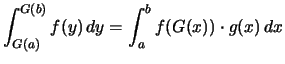 .
.
Bemerkung zum Beweis:
![[*]](crossref.png) gleich 0.
gleich 0.![[*]](crossref.png) ).
).
Dann konvergieren die Stammfunktionen
![]() gleichmäßig gegen
gleichmäßig gegen ![]() :
:
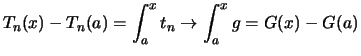 .
.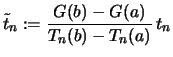 .
.
Beweis . Man wähle also eine Folge von
Treppenfunktionen ![]() mit Stammfunktionen
mit Stammfunktionen ![]() ,
so daß
,
so daß
![]() und
und
![[*]](crossref.png)
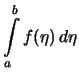 |
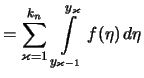 |
|
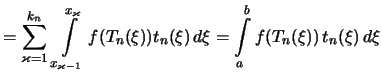 |
![[*]](crossref.png) folgt
die Gleichung:
folgt
die Gleichung:
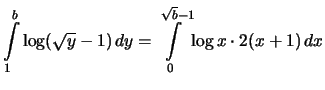 für
für
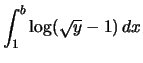 |
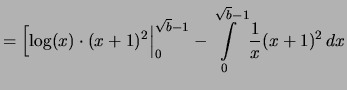 |
|
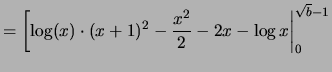 . . |
Beweis . Dies folgt aus der Abschätzung:
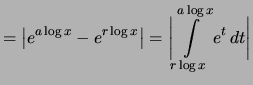 |
||
Man zeige mit Hilfe
der Substitution
![]() und
und
![]()
![]() :
:
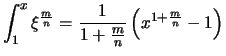 für
für
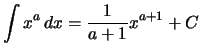 für
für
Bemerkung. Wenn der Exponent
![]() ist, so gilt
(2.) für
ist, so gilt
(2.) für
![]() .
.