




Next: Vollständig beschränkte Modulhomomorphismen
Up: Operatormoduln über C*-Algebren
Previous: Operatormoduln über C*-Algebren
Beispiele für Operatormoduln
- 1.
- Seien A eine unitale C*-Algebra, E ein normierter Raum und X ein Operatorraum. Dann sind B(E, A) resp.
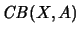 Operatorräume vermöge der Identifizierungen
Mn(B(E, A))=B(E, Mn(A)) resp.
Operatorräume vermöge der Identifizierungen
Mn(B(E, A))=B(E, Mn(A)) resp.
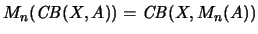 .
Diese werden zu A-Operatorbimoduln, stattet man sie mit den natürlichen Moduloperationen aus:
.
Diese werden zu A-Operatorbimoduln, stattet man sie mit den natürlichen Moduloperationen aus:
für alle
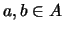 ,
,
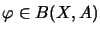 resp.
resp.
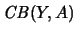 ,
,
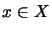 resp.
resp. 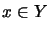 [ER88, p. 140].
[ER88, p. 140].
- 2.
- Sei
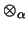 ein Operatorraum-Tensorprodukt . Seien A eine unitale C*-Algebra, X ein Operatorraum.
Der Operatorraum
ein Operatorraum-Tensorprodukt . Seien A eine unitale C*-Algebra, X ein Operatorraum.
Der Operatorraum
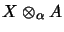 wird zu einem A-Operatorbimodul vermöge der Moduloperationen:
wird zu einem A-Operatorbimodul vermöge der Moduloperationen:
wobei 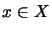 ,
a, b,
,
a, b, 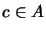 .
Speziell erhellt dies für das injektive Operatorraum-Tensorprodukt:
.
Speziell erhellt dies für das injektive Operatorraum-Tensorprodukt:
ist ein A-Operatorbimodul (vgl. Beispiel 1.).
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04