Operatormoduln über C^*-Algebren

Seien A₁, $A_2 \subset B(\mathcal{H})$ C^*-Algebren mit ${{\mathbb{1} }_{B(\mathcal{H})}} \in A_1, A_2$. Ein abgeschlossener Unterraum X in ${B(\mathcal{H})}$ heißt     konkreter (A₁,A₂)-Operatormodul  , falls $A_1X \subset X$ und $XA_2 \subset X$. Im Falle A₁=A₂=A nennen wir X einen   konkreten A-Operatorbimodul (vgl. [ER88, p. 137]).

Analog zu den Operatorräumen und den Operatoralgebren lassen sich auch Operatormoduln über C^*-Algebren abstrakt charakterisieren (vgl. [Pop98, Déf. 4.1]):
Seien wie oben A₁, $A_2 \subset B(\mathcal{H})$ unitale C^*-Algebren mit ${{\mathbb{1} }_{B(\mathcal{H})}} \in A_1$, A₂, ferner X (algebraisch) ein (A₁,A₂)-Modul. Dann nennen wir X einen   abstrakten (A₁,A₂)-Operatormodul, falls er eine Operatorraum-Struktur trägt, die den folgenden     (Ruanschen) Axiomen genügt:

(R1)	$\Vert axb\Vert _m$	$\leq$	$\Vert a\Vert \Vert x\Vert _m \Vert b\Vert$
(R2)	$\left\Vert \left( \begin{array}{cc} x & 0 \\ 0 & y \end{array} \right) \right\Vert _{m+n}$	=	${\rm {max}} \{ \Vert x\Vert _m, \Vert y\Vert _n \},$

wobei $m, n \in {\mathbb{N} }$, $a \in M_m(A_1)$, $x \in M_m(X)$, $y\in M_n(Y)$, $b \in M_m(A_2)$.

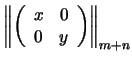Für abstrakte Operatormoduln gilt ein     Darstellungssatz vom Ruan-Typ (vgl. [Pop98, Thm. 4.7]):

Seien $A_1, A_2 \subset B(\mathcal{H})$ unitale C^*-Algebren mit ${{\mathbb{1} }_{B(\mathcal{H})}} \in A_1, A_2$, ferner V ein abstrakter (A₁,A₂)-Operatormodul. Dann existieren ein Hilbertraum $\mathcal{K}$, eine vollständige Isometrie $\Theta: X \hookrightarrow B(\mathcal{K})$ und ^*-Darstellungen $\pi_1$, $\pi_2$ von A₁ bzw. A₂ auf K, so daß gilt:

$$\Theta(axb) = \pi_1(a) \Theta(x) \pi_2(b),$$

wobei $x \in X$, $a \in A_1$, $b \in A_2$. Im Falle A₁=A₂ kann man sogar $\pi_1=\pi_2$ wählen.