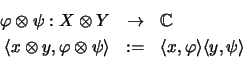Next: Injektives Operatorraum-Tensorprodukt
Up: Operatorraum-Tensorprodukte
Previous: Duales Operatorraum-Tensorprodukt
Kreuznormen
Eine Operatorraum-Norm
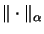 auf
auf
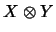 heißt
Kreuznorm,
wenn
heißt
Kreuznorm,
wenn
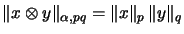 für alle
für alle
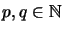 ,
,
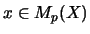 ,
,
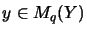 gilt.
gilt.
Für Kreuznormen ist
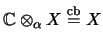 vollständig isometrisch.
vollständig isometrisch.
Zuweilen betrachtet man nur ein Operatorraum-Norm
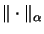 auf dem algebraischen
Tensorprodukt zweier Operatorräume X und Y.
Dann verlangt man zumindest die folgenden Eigenschaften
(i)-(iii).24
Operatorraum-Tensornormen haben immer diese Eigenschaften.
auf dem algebraischen
Tensorprodukt zweier Operatorräume X und Y.
Dann verlangt man zumindest die folgenden Eigenschaften
(i)-(iii).24
Operatorraum-Tensornormen haben immer diese Eigenschaften.
- (i)
-
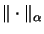 ist eine Kreuznorm.
ist eine Kreuznorm.
- (ii)
- Für Linearformen
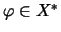 ,
,
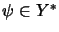 hat die Linearform
hat die Linearform
für
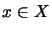 ,
,
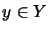 eine stetige lineare Fortsetzung auf
eine stetige lineare Fortsetzung auf
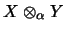 .
.
-
- Die duale Operatorraum-Norm
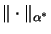 wird durch die vollständig isometrische Einbettung
wird durch die vollständig isometrische Einbettung
definiert.
- (iii)
-
Die duale Norm
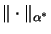 ist eine Kreuznorm.
ist eine Kreuznorm.
Unter den Operatorraum-Normen auf
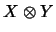 ,
für die
,
für die
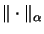 und
und
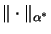 Kreuznormen sind,
gibt es eine kleinste, die
injektive
Operatorraum-Tensornorm
Kreuznormen sind,
gibt es eine kleinste, die
injektive
Operatorraum-Tensornorm
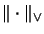 ,
und eine größte, die
projektive
Operatoraum-Tensornorm
,
und eine größte, die
projektive
Operatoraum-Tensornorm
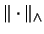 [BP91, Prop. 5.10].
Auf dem algebraischen Tensorprodukt
[BP91, Prop. 5.10].
Auf dem algebraischen Tensorprodukt
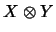 kann man diese mit der
injektiven Tensornorm
kann man diese mit der
injektiven Tensornorm
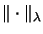 und der projektiven Tensornorm
und der projektiven Tensornorm
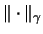 normierter Räume vergleichen:
normierter Räume vergleichen:





Next: Injektives Operatorraum-Tensorprodukt
Up: Operatorraum-Tensorprodukte
Previous: Duales Operatorraum-Tensorprodukt
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() vollständig isometrisch.
vollständig isometrisch.
![]() auf dem algebraischen
Tensorprodukt zweier Operatorräume X und Y.
Dann verlangt man zumindest die folgenden Eigenschaften
(i)-(iii).24
Operatorraum-Tensornormen haben immer diese Eigenschaften.
auf dem algebraischen
Tensorprodukt zweier Operatorräume X und Y.
Dann verlangt man zumindest die folgenden Eigenschaften
(i)-(iii).24
Operatorraum-Tensornormen haben immer diese Eigenschaften.