




Next: Projektives Operatorraum-Tensorprodukt
Up: Injektives Operatorraum-Tensorprodukt
Previous: Formeln für das injektive
Ein Operatorraum X heißt exakt [Pis95, §1], wenn mit der kurzen exakten Sequenz
auch die Sequenz der injektiven Tensorprodukte
wieder exakt ist.
Ein solcher Operatorraum läßt beliebige
exakte Sequenzen von C*-Algebren beim Tensorieren exakt
(für C*-Algebren siehe [Kir83]).
Offensichtlich sind alle endlichdimensionalen Räume exakt.
Exaktheit vererbt sich auf Unterräume. Ebenso ist
das injektive Tensorprodukt zweier exakter Operatorräume
wieder exakt.
Für alle exakten Räume X ist
durch die Größe
ein Exaktheitsgrad gegeben, und es gilt
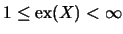 [Pis95, §1],
da die Abbildung
[Pis95, §1],
da die Abbildung
eine vollständige Kontraktion ist.
Für nicht exakte Operatorräume X vereinbart man ex
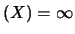 .
.
Für eine exakte C*-Algebra A ist immer ex(A)=1.
26
Für einen Operatorraum X gilt:
weshalb man sich bei der Untersuchung der Exaktheit auf endlichdimensionale
Räume beschränken kann. Daraus folgt auch unmittelbar: ex
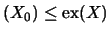 ,
wenn
,
wenn
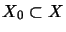 .
Für endlichdimensionale Operatorräume läßt sich
mit der vollständigen Variante der Banach-Mazur-Distanz
.
Für endlichdimensionale Operatorräume läßt sich
mit der vollständigen Variante der Banach-Mazur-Distanz
( das Infimum wird dabei über alle Isomorphismen 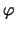 von
X1 nach X2 gebildet ) die Größe
von
X1 nach X2 gebildet ) die Größe
definieren27.
Nach [Pis95, Thm. 1] gilt : ex
(X)=dSK(X) , und es ist
ex
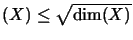 .
.





Next: Projektives Operatorraum-Tensorprodukt
Up: Injektives Operatorraum-Tensorprodukt
Previous: Formeln für das injektive
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() .
.