C^*-Konvexität

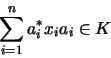
Eine C^*-konvexe Menge ist eine Teilmenge K einer unitalen C^*-Algebra A, so daß

$$\sum_{i=1}^{n} a_i^*x_ia_i \in K$$

für alle $x_i\in K$ und $a_i\in A$ mit $\sum_{i=1}^{n} a_i^*a_i = {\mathbb{1} }$.

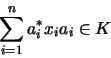
Dabei heißt eine Summe der Form $\sum_{i=1}^{n} a_i^*x_ia_i$ C^*-Konvexkombination.

Eine C^*-absolutkonvexe Menge ist eine Teilmenge K einer C^*-Algebra A, so daß

$$\sum_{i=1}^{n} a_i^*x_ib_i \in K$$

für alle $x_i\in K$ und a_i, $b_i \in A$ mit $\sum_{i=1}^{n} a_i^*a_i$, $\sum_{i=1}^n b_i^*b_i \leq {\mathbb{1} }$ [Mag98a].

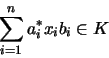
Insbesondere sind C^*-konvexe Mengen konvex, und C^*-absolutkonvexe Mengen sind absolutkonvex.

Beispiele für C^*-konvexe Mengen: Sei $\mathcal{H}$ ein Hilbertraum und fest. Man definiert den Matrix-Wertevorrat

$$W(T)_n :=\{\varphi(T)\vert\varphi:B(\mathcal{H})\rightarrow M_n\mbox{ vollst\uml andig positiv und unital}\}.$$

W(T)_n ist eine kompakte und C^*-konvexe Teilmenge von M_n.

Zu jeder kompakten C^*-konvexen Teilmenge K von M_n existiert ein separabler Hilbertraum $\mathcal{H}$ und $S\in B(\mathcal{H})$ mit K=W(S)_n (vgl. [LP81, Prop. 31]).

Desweiteren sind die Mengen

$$\mathrm{Ball}(B(\mathcal{H}))=\{x\in B(\mathcal{H})\vert\Vert... ...\quad } P=\{x\in B(\mathcal{H})\vert\leq x\leq {\mathbb{1} }\}$$

C^*-konvexe und WOT-kompakte Teilmengen von ${B(\mathcal{H})}$. $\mathrm{Ball}(B(\mathcal{H}))$ ist zusätzlich C^*-absolutkonvex.

C^*-konvexe Mengen wurden von Loebl und Paulsen in [LP81] eingeführt und Anfang der neunziger Jahre insbesondere von Farenick und Morenz ([Far92],[FM93]) untersucht. Diese Untersuchungen beschäftigten sich mit der Frage nach einer Analogie zum Satz von Krein-Milman. Schließlich gelang es Morenz eine solche zu zeigen [Mor94, Th. 4.5]. Ende der neunziger Jahre variierte Magajna die Definition von C^*-konvex leicht und zeigte einige Trennungssätze [Mag98a, Th. 1.1] und auch eine Analogie zum Satz von Krein-Milman [Mag98b, Th. 1.1].