




Next: C*-extremale Punkte
Up: C*-Konvexität
Previous: C*-Konvexität
Seien
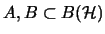 unitale C*-Algebren und
unitale C*-Algebren und
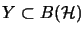 ein (A,B)-Bimodul. Dann heißt
ein (A,B)-Bimodul. Dann heißt
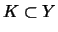 (A,B)-absolutkonvex, wenn
(A,B)-absolutkonvex, wenn
für alle 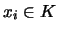 und
und 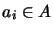 ,
,
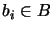 mit
mit
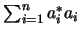 ,
,
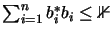 .
Sei Y ein A-Bimodul. Dann heißt K A-konvex, wenn
.
Sei Y ein A-Bimodul. Dann heißt K A-konvex, wenn
für alle 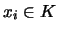 und
und 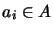 mit
mit
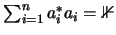 .
Im Fall Y=A stimmt diese Definition also mit der von C*-konvexen Mengen überein.
.
Im Fall Y=A stimmt diese Definition also mit der von C*-konvexen Mengen überein.
Es gelten folgende Trennungssätze [Mag98a, Thm. 1.1]: Seien
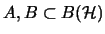 unitale C*-Algebren und
unitale C*-Algebren und
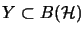 ein
(A,B)-Bimodul. Sei
ein
(A,B)-Bimodul. Sei
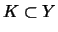 normabgeschlossen und
normabgeschlossen und
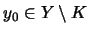 .
.
- 1.
- Wenn A=B,
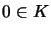 und K A-konvex, dann existieren ein Hilbertraum
und K A-konvex, dann existieren ein Hilbertraum
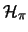 ,
eine zyklische Darstellung
,
eine zyklische Darstellung
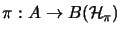 und ein vollständig beschränkter
A- Bimodul-Homomorphismus
und ein vollständig beschränkter
A- Bimodul-Homomorphismus
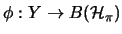 ,
so daß für alle
,
so daß für alle 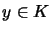
- 2.
- Wenn K (A,B)-absolutkonvex ist, dann existieren ein Hilbertraum
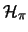 ,
Darstellungen
,
Darstellungen
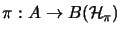 und
und
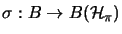 und ein vollständig beschränkter (A,B)- Bimodul-Homomorphismus
und ein vollständig beschränkter (A,B)- Bimodul-Homomorphismus
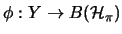 ,
so daß für alle
,
so daß für alle 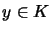
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
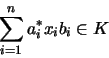
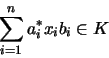
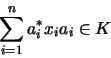
![]() unitale C*-Algebren und
unitale C*-Algebren und
![]() ein
(A,B)-Bimodul. Sei
ein
(A,B)-Bimodul. Sei
![]() normabgeschlossen und
normabgeschlossen und
![]() .
.