Vollständig integrale Abbildungen

Vollständig integrale Abbildungen definiert man unter Zuhilfenahme der vollständig nuklearen Abbildungen . Eine Abbildung $\varphi:X\to Y$ heißt      vollständig integral, wenn es eine Konstante c>0 und ein Netz von endlichrangigen $\varphi_\alpha \in \mathit{CN}(X,Y)$ gibt mit $\nu(\varphi_\alpha)\leq c$, das gegen $\varphi$ in der Punkt-Norm-Topologie ⁵⁷ konvergiert.

Die Menge aller dieser Abbildungen bildet den Raum   $\mathit{CI}(X,Y)$ der vollständig integralen Abbildungen.

Es gibt die kleinste all dieser Konstanten c, die die obige Bedingung erfüllen, die mit   $\iota(\varphi)$ bezeichnet wird. $\iota(\cdot)$ definiert eine Norm, mit der $\mathit{CI}(X,Y)$ zu einem Banachraum wird. Die Einheitskugel von $\mathit{CI}(X,Y)$ ist also gerade der Punkt-Norm-Abschluß der Einheitskugel von $\mathit{CN}(X,Y)$.

Die kanonische Operatorraumstruktur erhält man, indem man die Einheitskugel von $M_n(\mathit{CI}(X,Y))$ als Punkt-Norm-Abschluß der Einheitskugel von $M_n(\mathit{CN}(X,Y))$ setzt.

Es gilt nach Definition $\iota(\varphi)\leq\nu(\varphi)$; bei endlichdimensionalem X ist sogar [EJR98, Lemma 4.1]

$$\mathit{CI}(X,Y)\stackrel{\mathrm{cb}}{=}\mathit{CN}(X,Y)\mbox{.}$$

Integrale ⁵⁸ Abbildungen sind vollständig integral [ER94, 3.10].

Die   kanonische Einbettung

$$\mathit{CI}(X,Y)\hookrightarrow (X \stackrel{\scriptscriptstyle\vee}{\otimes}Y^*)^*$$

ist eine vollständige Isometrie [EJR98, Cor. 4.3]. Man hat ferner [EJR98, Cor. 4.6] $\varphi$ ist genau dann   vollständig integral, wenn es eine Faktorisierung der Form:

$$\begin{eqnarray*}B({\cal H}) & \stackrel{M(\omega)}{\rightarrow} & B({\cal K})^*... ... & \stackrel{\varphi}{\rightarrow} Y\hookrightarrow& Y^{**} \\ \end{eqnarray*}$$

mit schwach^*-stetigem s gibt. Die Abbildung $M(\omega):B({\cal H})\to B({\cal K})^*$ ist für zwei Elemente $a\in B({\cal H})$, $b\in B({\cal K})$ über $(M(\omega)(a))(b)=\omega(a\otimes b)$ definiert. Für die Norm gilt: $\iota(\varphi)= 1$, wenn es eine Faktorisierung mit $\Vert r\Vert _{cb}\Vert\omega \Vert\Vert s\Vert _{cb}= 1$ gibt (man beachte i.a. $\Vert M(\omega)\Vert _{cb}\neq\Vert\omega\Vert$).

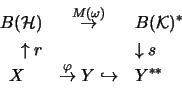
Die vollständig integralen Abbildungen erfüllen ebenfalls die $\mathit{CB}$-Idealeigenschaft . Im Gegensatz zu den vollständig nuklearen Abbildungen sind sie aber lokal . Man hat aber im allgemeinen nur $\iota(\varphi)\leq\iota(\varphi^*)$ [EJR98].