Vollständig nukleare Abbildungen

Seien X und Y Operatorräume. Die      vollständig nuklearen Abbildungen von X nach Y [ER94, §2], [EJR98, §3], werden über die   projektive Operatorraumtensornorm erklärt. Man betrachtet die Fortsetzung der kanonischen Identität $X^* \otimes Y = F(X,Y)$:

$$\Phi :X^*\stackrel{\scriptscriptstyle\wedge}{\otimes}Y\righta... ...ckrel{\scriptscriptstyle\vee}{\otimes}Y\subset CB(X,Y)\mbox{.}$$

Es ist $\stackrel{\scriptscriptstyle\vee}{\otimes}$ das injektive Tensorprodukt und $\stackrel{\scriptscriptstyle\wedge}{\otimes}$ das projektive Tensorprodukt .

Eine Abbildung heißt vollständig nuklear, wenn sie im Bild von $\Phi$ liegt. Man bezeichnet mit  

$$\mathit{CN}(X,Y):=(X^*\stackrel{\scriptscriptstyle\wedge}{\otimes}Y)/ {\rm Kern}(\Phi)$$

den Raum der vollständig nuklearen Abbildungen und versieht ihn mit der Quotienten operatorraumstruktur. Die Operatorraumnorm wird mit   $\nu(\cdot)$ bezeichnet. $M_n(\mathit{CN}(X,Y))$ und $\mathit{CN}(X,M_n(Y))$ sind i.a. nicht isometrisch.

Nukleare ⁵⁵ Abbildungen sind vollständig nuklear. [ER94, 3.10]

Die projektive Tensornorm erhält i.a. keine vollständigen Isometrien. Deshalb ist (anders als bei den vollständig beschränkten Abbildungen) auch für Unterräume $Y_o\subset Y$ die kanonische Einbettung $\mathit{CN}(X,Y_0)\to \mathit{CN}(X,Y)$i.a. nur vollständig kontrahierend und nicht isometrisch. Da die projektive Tensornorm Quotientenabbildungen erhält, gibt es zu jeder nuklearen Abbildung $\varphi:X_0\to Y$ mit $\nu(\varphi)<1$, von einem Unterraum $X_0\subset X$ eine Fortsetzung $\tilde{\varphi}$auf ganz X mit $\nu(\tilde{\varphi})<1$. Die vollständig nuklearen Abbildungen haben die $\mathit{CB}$-Idealeigenschaft . Weiter ist mit $\varphi$ auch $\varphi^*$ vollständig nuklear, und es gilt: $\nu(\varphi^*)\leq\nu(\varphi)$ [EJR98, Lemma 3.2].

  Eine Abbildung $\varphi$ ist genau dann vollständig nuklear, wenn es eine Faktorisierung der Form

$$\begin{eqnarray*}B(\ell_2) & \stackrel{M(a,b)}{\rightarrow} & T(\ell_2) \\ \up... ...downarrow s\\ X\quad & \stackrel{\varphi}{\rightarrow} & Y \\ \end{eqnarray*}$$

gibt. Dabei sind a, b Hilbert-Schmidt-Operatoren und definieren die Abbildung $M(a,b): x \mapsto a x b$. Für die vollständig nukleare Norm gilt dann: $\nu (\varphi )=1$ genau dann, wenn für alle $\epsilon>0$ ein Diagramm mit $\Vert r\Vert _{cb}\Vert a\Vert _2\Vert b\Vert _2\Vert s\Vert _{cb}\leq 1+\epsilon$ existiert ⁵⁶ [ER94, Thm. 2.1].

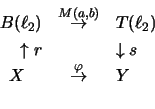
Man beachte, daß die vollständig nuklearen Abbildungen nicht lokal sind.