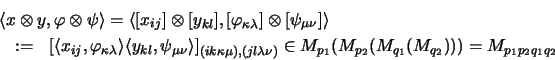Die Matrix-Dualität, die der Dualitätstheorie der Operatorräume zugrundeliegt, ist ein Spezialfall der allgemeinen Amplifikation einer bilinearen Abbildung.
Die allgemeine Amplifikation einer Dualität
![]() von Vektorräumen ist demgemäß definiert als
von Vektorräumen ist demgemäß definiert als
Liest man ![]() als Abbildung
als Abbildung
![]() so gilt
so gilt