




Next: Allgemeine Amplifikation einer Dualität
Up: Tensorprodukte
Previous: Tensorprodukte
Tensorprodukt von Operatormatrizen
Wie üblich erklären wir das algebraische Tensorprodukt von Operatormatrizen
![$x = [x_{ij}] \in M_{p}(X)$](img541.gif) ,
,
![$y = [y_{kl}] \in M_{q}(Y)$](img542.gif) durch
durch
Hierbei wurde die Definition
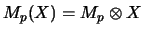 und das Assoziativgesetz
und das Assoziativgesetz
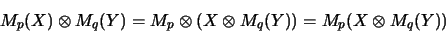 |
(5) |
benutzt.
Für die weitere Identifikation beachte man, daß die
shuffle-Abbildung ein algebraischer Isomorphismus ist:
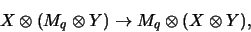 |
(6) |
für
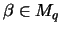 ,
,
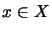 ,
,
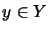 .
Mit Hilfe des shuffle-Isomorphismus
identifizieren wir weiter:
.
Mit Hilfe des shuffle-Isomorphismus
identifizieren wir weiter:
Zuletzt identifizieren59
wir noch wie üblich
Mp(Mq) = Mpq
und erhalten
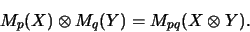 |
(7) |
Wir nennen diesen algebraischen Isomorphismus den
shuffle-Isomorphismus
Man beachte, daß für Operatorraum-Tensorprodukte die
algebraischen Identifikationen
(5) und (6)
nur vollständige Kontraktionen sind:
Im allgemeinen sind dies nicht einmal auf der Grundstufe Isometrien.
Für ein Operatorraum-Tensorprodukt ist also die
shuffle-Abbildung
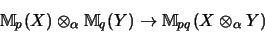 |
(10) |
im allgemeinen
nur
vollständig kontrahierend.
Im Falle des
injektiven Operatorraum-Tensorproduktes
ist dies natürlich eine vollständige Isometrie.
Man betrachtet die shuffle-Abbildung allgemeiner für
Rechteckmatrizen60:
Ein Beispiel ist auch die
Gleichung von Blecher und Paulsen.





Next: Allgemeine Amplifikation einer Dualität
Up: Tensorprodukte
Previous: Tensorprodukte
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() ,
,
![]() durch
durch