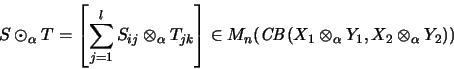Bei der Definition von
vollständig beschränkten
bilinearen Abbildungen und der Bildung des
Haagerup-Tensorproduktes
verwendet man die
tensorielle
Matrixmultiplikation
[Eff87]
Die
Amplifikation
der bilinearen Abbildung
![]() ist
ist
Für skalare Matrizen
![]() ,
,
![]() gilt
gilt
Für lineare Abbildungen
![\begin{eqnarray*}\Phi = [\Phi_{ij}] : \, x &\rightarrow& M_{n,l}(V) \mbox{,}\\
\Psi = [\Phi_{jk}] : \, x &\rightarrow& M_{l,n}(W)\\
\end{eqnarray*}](img984.gif)
![\begin{displaymath}\Phi \odot \Psi =
\left[\sum_{j=1}^l \Phi_{ij} \otimes \Psi_{jk}\right] :
X \otimes Y \rightarrow M_{n}(V \otimes W),
\end{displaymath}](img986.gif)
![\begin{displaymath}\Phi \odot \Psi : x \otimes y \mapsto
\left[\sum_{j=1}^l \Phi_{ij}(x) \otimes \Psi_{jk}(y) \right].
\end{displaymath}](img987.gif)
Es sei
![]() ein
Operatorraum-Tensorprodukt .
Wir definieren die
tensorielle Matrixmultiplikation
ein
Operatorraum-Tensorprodukt .
Wir definieren die
tensorielle Matrixmultiplikation
![]() von Operatormatrizen
von Operatormatrizen
![]() ,
,
![]() vollständig beschränkter Abbildungen als
vollständig beschränkter Abbildungen als