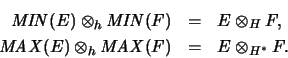Haagerup-Tensorprodukt

  Das  Haagerup -Tensorprodukt von C^*-Algebren wurde von Effros und Kishimoto [EK87] eingeführt. Es verallgemeinert eine Untersuchung von U. Haagerup [Haa80].

Es seien A, B C^*-Algebren in ${B(\mathcal{H})}$. Auf dem algebraischen Tensorprodukt $A \otimes B$ ist die Haagerup-Tensornorm definiert durch

$$\mbox{$ \Vert u\Vert _h := \inf\left\{ \left\Vert \sum_{\n... ...\ \ :\ u = \sum_{\nu=1}^n a_\nu \otimes b_\nu \right \}$ },$$

wobei $n\in{\mathbb{N} }$, $a_\nu \in A$, $b_\nu \in B$ sind.

Die Haagerup-Norm von $\sum_{\nu=1}^n a_\nu \otimes b_\nu \in A \otimes B$ ist gleich der cb-Norm des elementaren Operators $B(\mathcal{H}) \ni x \mapsto \sum_{\nu=1}^n a_\nu x b_\nu$.

Die folgende Definition liefert eine vollständig isometrische Einbettung $A \otimes_h B \hookrightarrow \mathit{CB}(B(\mathcal{H}))$.

Für Operatorräume X, Y ist die  Haagerup -Operatorraum-Tensornorm     von $u \in M_n(X\otimes Y)$ definiert durch (vgl. [ER91, Formel (2.11)], [BP91, Lemma 3.2])

$$\Vert u\Vert _h = \inf \Vert x\Vert _{n,l}\ \Vert y\Vert _{l,n},$$

wobei $l \in {\mathbb{N} }$, $x \in M_{n,l}(X)$, $y \in M_{l,n}(Y)$ sind und u gleich dem tensoriellen Matrixprodukt $u = x \odot y$ ist. Es gibt weitere nützliche Formeln 1 2 und 3 für die Haagerup-Norm.

Dem Haagerup-Tensorprodukt entsprechen die vollständig beschränkten bilinearen Abbildungen. Für den Dual gilt

$$(X\otimes_h Y)^* \stackrel{\mathrm{cb}}{=}\mathit{CB}(X \times Y;{\mathbb{C} }).$$

Für einen Operatorraum Z gilt vollständig isometrisch

$$\mathit{CB}(X \otimes_h Y; Z) \stackrel{\mathrm{cb}}{=}\mathit{CB}(X \times Y; Z).$$

Das Haagerup-Tensorprodukt ist nicht symmetrisch , wie Beispiele zeigen. Es ist aber assoziativ , injektiv [PS87, p. 272; Thm. 4.4], [BP91, Thm. 3.6], projektiv [ER91, Thm. 3.1] und selbstdual [ER91, Thm. 3.2]. Also ist die Einbettung

$$X^* \otimes_h Y^* \hookrightarrow (X \otimes_h Y)^*$$

vollständig isometrisch. Die stetige Fortsetzung der identischen Abbildung des algebraischen Tensorproduktes zweier Operatorräume X, Y vom Haagerup-Tensorprodukt in das injektive Tensorprodukt ist injektiv. Man hat also eine kanonische Einbettung

$$X \otimes_h Y \subset X \stackrel{\scriptscriptstyle\vee}{\otimes} Y.$$

Die komplexe Interpolation von Operatorräumen und die Bildung des Haagerup-Tensorproduktes vertauschen [Pis96, Thm. 2.3]. Es seien (X₀,X₁) und (Y₀,Y₁) verträgliche Paare von Operatorräumen. Dann ist $(X_0 \otimes _h Y_0, X_1 \otimes Y_1)$ ein verträgliches Paar von Operatorräumen und es gilt vollständig isometrisch

$$(X_0 \otimes _h Y_0, X_1 \otimes Y_1)_\vartheta \stackrel{\mathrm{cb}}{=} (X_0,X_1)_\vartheta \otimes_h (Y_0,Y_1)_\vartheta$$

für $0 \leq \vartheta \leq 1$.

Auf normierten Räumen gibt es keine Tensornorm, die zugleich assoziativ, injektiv, projektiv, selbstdual ist. Das Haagerup-Tensorprodukt kann man als eine Verallgemeinerung       des von Grothendieck eingeführten H-Tensorproduktes ²⁹ normierter Räume E, F auffassen [BP91, pp. 277-279, Prop. 4.1]. Auf der Grundstufe gilt nämlich isometrisch:

$$\begin{eqnarray*}\mathit{MIN}(E)\otimes_h \mathit{MIN}(F) &=& E \otimes_H F, \\ \mathit{MAX}(E)\otimes_h \mathit{MAX}(F) &=& E \otimes_{H^*} F. \end{eqnarray*}$$

Die Nichtassoziativität des H-Tensorproduktes spiegelt sich darin wieder, daß im allgemeinen $\mathit{MIN}(E)\otimes_h \mathit{MIN}(F)$ und $\mathit{MIN}(E \otimes_H F)$ nicht vollständig isometrisch sind.