



Nächste Seite: Gleichmäßige Stetigkeit
Aufwärts: Stetige Funktionen auf kompakten
Vorherige Seite: Stetige Funktionen auf kompakten
Inhalt
Satz vom Maximum
Bemerkung 2.6.1
- Die beiden Sätze dieses Abschnittes gelten allgemeiner
für stetige reelle Funktionen auf kompakten Teilmengen der reellen Zahlen.
Die Intervalleigenschaft ist unwichtig.
Auch die Beweise kann man sinngemäß übernehmen.
- Die Sätze gelten sogar für beliebige kompakte Mengen.
Man führt dann sehr ähnliche Beweise, in denen man statt des
Supremumsprinzips den Satz von
Bolzano-Weierstraß verwendet (vgl. Abschnitt
![[*]](crossref.png) )
)
- Wir konstruieren im Beweis des Satzes vom Maximum den grösten Punkt,
in dem die Funktion ihr Maximum annimmt.
Verwendet man stattdessen den Satz von Bolzano-Weierstraß, so findet man nur
irgendein Maximum.
Lemma 2.6.2 (Beschränktheits-Lemma)
Es sei
![$ [a,b] \subset \mathbb{R}$](img1833.png) ein kompaktes Intervall.
Dann ist jede stetige Funktion
ein kompaktes Intervall.
Dann ist jede stetige Funktion
![$ f: [a,b] \rightarrow \mathbb{R}$](img1742.png) beschränkt.
beschränkt.
Bemerkung. Der Satz wird mit einem Widerspruchsbeweis gezeigt.
Beweis (Beschränktheits-Lemma).
Annahme:
![$ f: [a,b] \rightarrow \mathbb{R}$](img1742.png) ist nach oben unbeschränkt.
ist nach oben unbeschränkt.
Man bilde zu
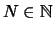 die nichtleere Menge
die nichtleere Menge 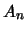 :
:
Nach Lemma ![[*]](crossref.png) existiert
existiert
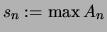 .
.
Da
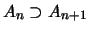 , ist die Folge
, ist die Folge 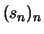 monoton fallend.
Es existiert
monoton fallend.
Es existiert
![$\displaystyle [a,b]\ni c= \lim_{n\to\infty}s_n$](img1840.png) .
.
Da 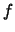 stetig ist, folgt ein Widerspruch:
stetig ist, folgt ein Widerspruch:
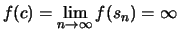 .
.
Satz 2.6.3 (Satz vom Maximum)
Es sei
![$ [a,b] \subset \mathbb{R}$](img1833.png) ein nichtleeres, kompaktes Intervall.
Dann nimmt jede stetige Funktion
ein nichtleeres, kompaktes Intervall.
Dann nimmt jede stetige Funktion
![$ f: [a,b] \rightarrow \mathbb{R}$](img1742.png) ein Maximum an.
ein Maximum an.
D.h., es gibt mindestens ein
![$ \xi \in [a,b] $](img1842.png) so, daß für alle
so, daß für alle
![$ x \in [a,b] $](img1843.png) gilt:
gilt:
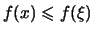 .
.
KARL WEIERSTRASS (1815-1897)
Bemerkung.
Analog gilt, daß jede stetige Funktion auf einem kompakten Intervall
ein Minimum hat.
Die kompaktheit des Intervalls ist eine unverzichtbare Vorrausetzung
für den Satz vom Maximum:
Beispiele 2.6.4
Mit der Wackelfunktion
![[*]](crossref.png)
(
![[*]](crossref.png)
)
bilde man die Funktion
![$\displaystyle V: (0,1] \ni x \mapsto (1-x)W(x)$](img1845.png) .
.
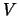
ist auf
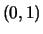
stetig und beschränkt und hat auf
![$ (0,1] $](img1848.png)
weder ein Maximum noch ein Minimum.
Es gilt
Man kann
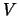
nicht stetig in
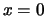
fortsetzen und auch
keinen Funktionswert bei
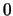
so festsetzen, daß
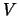
Maximum
und Minimum hat.
Mit Korollar ![[*]](crossref.png) ergibt sich das Korollar:
ergibt sich das Korollar:
Korollar 2.6.5 (Stetiges Bild eines kompakten Intervalls)
Sei
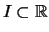 ein kompaktes Intervall und
ein kompaktes Intervall und
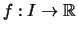 eine stetige Funktion.
Dann ist
eine stetige Funktion.
Dann ist 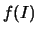 ein kompaktes Intervall.
ein kompaktes Intervall.
Beweis (Satz vom Maximum).
Nach Lemma ![[*]](crossref.png) ist
ist
![$ f: [a,b] \rightarrow \mathbb{R}$](img1742.png) ist nach oben beschränkt:
ist nach oben beschränkt:
![$\displaystyle s :=\sup \{ f(x) \mid x \in [a,b] \} \in \mathbb{R}$](img1854.png) .
.
Man bilde zu
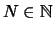 die nichtleere Menge
die nichtleere Menge 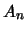 :
Nach Lemma
:
Nach Lemma ![[*]](crossref.png) existiert
existiert
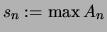 .
.
Da
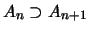 , ist die Folge
, ist die Folge 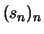 monoton fallend.
Es existiert
monoton fallend.
Es existiert
![$\displaystyle [a,b]\ni c= \lim_{n\to\infty}s_n$](img1840.png) .
.
Da 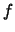 stetig ist, folgt
stetig ist, folgt
![$\displaystyle f(c) = \lim_{n\to\infty}f(s_n) = s = \sup\limits_{x\in[a,b]} f(x)$](img1857.png) .
.




Nächste Seite: Gleichmäßige Stetigkeit
Aufwärts: Stetige Funktionen auf kompakten
Vorherige Seite: Stetige Funktionen auf kompakten
Inhalt
Analysis1-A.Lambert
2001-02-09
![[*]](crossref.png) )
)
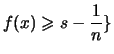 .
.