Es sei
![]() ein Intervall. Eine Funktion
ein Intervall. Eine Funktion
![]() heißt gleichmäßig stetig
wenn folgende gilt:
heißt gleichmäßig stetig
wenn folgende gilt:
Zu jedem
![]() gibt es ein
gibt es ein ![]() , so daß für alle
, so daß für alle
![]() ,
, ![]() aus
aus
![]() stets
stets
![]() folgt.
folgt.
In Zeichen:
Es sei
![]() ein Intervall. Eine Funktion
ein Intervall. Eine Funktion
![]() heißt gleichmäßig stetig
wenn folgende gilt:
heißt gleichmäßig stetig
wenn folgende gilt:
Zu jedem
![]() gibt es ein
gibt es ein ![]() , so daß für alle
, so daß für alle
![]() ,
, ![]() aus
aus
![]() stets
stets
![]() folgt.
folgt.
In Zeichen:
Bemerkung. Die Feststellungen
![[*]](crossref.png) und
und
![[*]](crossref.png) gelten sinngemäß auch für die Definition der Gleichmäßigen Stetigkeit.
gelten sinngemäß auch für die Definition der Gleichmäßigen Stetigkeit.
Was heißt es, daß eine Funktion nicht gleichmäßig stetig ist?
Es gibt ein
![]() , so daß es zu jedem
, so daß es zu jedem
![]() zwei Punkte
zwei Punkte
![]() ,
, ![]() gibt mit
gibt mit
![]() und
und
![]() .
.
In Zeichen:
Die Funktion ![]() ist nicht gleichmäßig stetig, wenn es ein
ist nicht gleichmäßig stetig, wenn es ein
![]() und zwei Folgen
und zwei Folgen ![]() ,
, ![]() in
in ![]() so gibt, daß
so gibt, daß
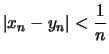 und
und
Beweis .
![[*]](crossref.png) (2) und
Bemerkung
(2) und
Bemerkung ![[*]](crossref.png) (
(![[*]](crossref.png) ) streng konkav.
Die Steigung ist also streng monoton fallend.
) streng konkav.
Die Steigung ist also streng monoton fallend.
Für ![]() ist
ist ![]() und
und
![]() . Folglich gilt:
. Folglich gilt:
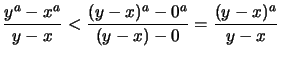 .
.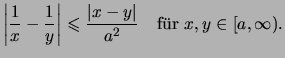
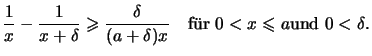
Es sei
![]() ein kompaktes Intervall.
Dann ist jede stetige Funktion
ein kompaktes Intervall.
Dann ist jede stetige Funktion
![]() gleichmäßig stetig.
gleichmäßig stetig.
Bemerkung. Der Satz wird mit einem Widerspruchsbeweis gezeigt.
EDUARD HEINE (1821-1861)
Beweis . Annahme:
![]() ist nicht gleichmäßig stetig.
ist nicht gleichmäßig stetig.
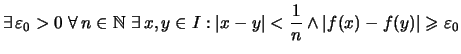 .
.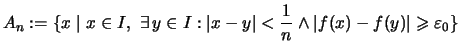 , , |
|
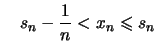 , , |
|
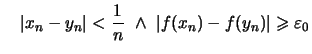 . . |
Übung. (Gleichmäßige Stetigkeit)
1.
Man modifiziere den Beweis von Satz ![[*]](crossref.png) oder den alternativen Beweis
im Beispiel
oder den alternativen Beweis
im Beispiel ![[*]](crossref.png) und zeige
die folgende Charakterisierung der gleichmäßigen Stetigkeit:
und zeige
die folgende Charakterisierung der gleichmäßigen Stetigkeit:
Es seien ![]() ein beschränktes Intervall und
ein beschränktes Intervall und
![]() .
Die folgenden Aussagen sind äquivalent:
.
Die folgenden Aussagen sind äquivalent:
2.
Man zeige, daß die Äquivalenz (1.) sinngemäß auch für Funktionen
![]() gilt.
gilt.
3.
Man zeige, daß der Fortsetzungssatz ![[*]](crossref.png) sinngemäß für gleichmäßig stetige Funktionen
sinngemäß für gleichmäßig stetige Funktionen
![]() gilt.
gilt.