




Next: Spalten und Zeilen eines
Up: Elementare Konstruktionen
Previous: Unterräume und Quotienten
Matrizen über einem Operatorraum
Der Vektorraum Mp(X) der
Matrizen über einem matrixnormierten
Raum X ist auf natürliche Weise
ebenfalls ein matrixnormierter Raum: Dabei wird die n-te Stufe
Mn(Mp(X)) durch die Identifikation
Mn(Mp(X)) = Mnp(X)
normiert [BP91, p. 265].
Mp(X), versehen mit dieser Operatorraumstruktur, bezeichnen wir7
mit
Insbesondere gilt für die Grundstufe
Entsprechend wird auch
Mp,q(X) durch die Identifizierung
Mn(Mp,q(X))=Mnp,nq(X)
zu einem matrixnormierten Raum
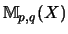 .
Dieser
ist durch Auffüllen der
Rechteckmatrizen mit Nullen ein Unterraum von
.
Dieser
ist durch Auffüllen der
Rechteckmatrizen mit Nullen ein Unterraum von
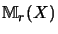 für
für
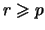 ,
q.
,
q.
Beispiele:
Ist A eine C*-Algebra, so ist
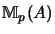 die C*-Algebra der
die C*-Algebra der 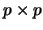 -Matrizen über A mit
ihrer Operatorraumstruktur.
-Matrizen über A mit
ihrer Operatorraumstruktur.
Der Banachraum Mp(A) ist die Grundstufe
des Operatorraumes
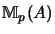 .
.
Die komplexen Zahlen haben genau eine Operatorraumstruktur, die auf
der Grundstufe isometrisch zu
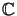 ist.
Für diese ist isometrisch
ist.
Für diese ist isometrisch
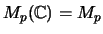 .
Wir setzen
.
Wir setzen
Damit bezeichnet
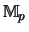 immer die C*-Algebra der
immer die C*-Algebra der
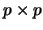 -Matrizen
mit ihrer Operatorraumstruktur.
Der Banachraum Mp ist die Grundstufe des Operatorraumes
-Matrizen
mit ihrer Operatorraumstruktur.
Der Banachraum Mp ist die Grundstufe des Operatorraumes
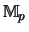 .
.





Next: Spalten und Zeilen eines
Up: Elementare Konstruktionen
Previous: Unterräume und Quotienten
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() die C*-Algebra der
die C*-Algebra der ![]() -Matrizen über A mit
ihrer Operatorraumstruktur.
-Matrizen über A mit
ihrer Operatorraumstruktur.
![]() .
.
![]() ist.
Für diese ist isometrisch
ist.
Für diese ist isometrisch
![]() .
Wir setzen
.
Wir setzen