![\begin{displaymath}\Vert T\Vert _{\mathrm{row}}
:=\sup_{n \in {\mathbb{N} }}
\s...
...ft\Vert\left[Tx_1 \ldots Tx_n\right]\right\Vert _{M_{1,n}(Y)}
\end{displaymath}](img168.gif)
![\begin{displaymath}\Vert T\Vert _{\mathrm{row}}
:=\sup_{n \in {\mathbb{N} }}
\s...
...ft\Vert\left[Tx_1 \ldots Tx_n\right]\right\Vert _{M_{1,n}(Y)}
\end{displaymath}](img168.gif)
![\begin{displaymath}\Vert T\Vert _{\mathrm{col}}
:=\sup_{n \in {\mathbb{N} }}
\s...
... \vdots \\ Tx_n \end{array}
\right]\right\Vert _{M_{n,1}(X)}
\end{displaymath}](img169.gif)
Wir haben die folgenden Charakterisierungen des Spalten-Hilbertraums
Ist X ein Operatorraum auf einem Hilbertraum
![]() ,
so sind äquivalent :
,
so sind äquivalent :
![]() vollständig isometrisch.
vollständig isometrisch.
![]() ist
ist
![]() und
für alle
und
für alle
![]() ist
ist
![]() .
.
![]() ist
ist
![]() und für alle
und für alle
![]() ist
ist
![]() .
.
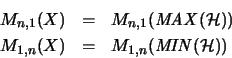
isometrisch.
Ist X ein Operatorraum, so sind äquivalent:
![]() ,
so daß
,
so daß
![]() vollständig isometrisch.
vollständig isometrisch.
![]()
und
![]()
isometrisch
[Mat94, Thm. 10].
![]() mit der Komposition als Multiplikation
ist eine Operatoralgebra
[Ble95, Thm. 3.4].
mit der Komposition als Multiplikation
ist eine Operatoralgebra
[Ble95, Thm. 3.4].