




Next: Bipolarensätze
Up: Matrixkonvexität
Previous: Beispiele
Ein wichtiges Hilfsmittel der Theorie sind die folgenden Trennungssätze.
Sei
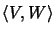 eine (nicht ausgeartete) Dualität von Vektorräumen. Dadurch
sind V und W mit schwachen Topologien versehen und die Matrizenstufen mit der
zugehörigen Produkttopologie. Zu
eine (nicht ausgeartete) Dualität von Vektorräumen. Dadurch
sind V und W mit schwachen Topologien versehen und die Matrizenstufen mit der
zugehörigen Produkttopologie. Zu
![$v=[v_{i,j}]\in M_n(V)$](img705.gif) und
und
![$w=[w_{k,l}]\in M_m(W)$](img706.gif) ist
ist
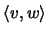 erklärt als die Amplifikation der Dualität:
erklärt als die Amplifikation der Dualität:
Man beachte, daß die Matrizen nicht total geordnet sind;
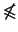 bedeutet also nicht >.
bedeutet also nicht >.
Satz:49
Sei
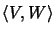 eine Dualität von Vektorräumen, K eine
abgeschlossene Menge von Matrizen über V, und
eine Dualität von Vektorräumen, K eine
abgeschlossene Menge von Matrizen über V, und
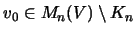 .
.
- a)
- [WW99, Thm. 1.6] Ist K matrixkonvex, so gibt es ein
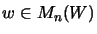 und
und
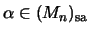 ,
so
daß für alle
,
so
daß für alle
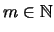 und
und 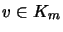
- b)
- [EW97b, Thm. 5.4] Ist K matrixkonvex und
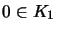 ,
so gibt es ein
,
so gibt es ein
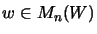 ,
so daß für alle
,
so daß für alle
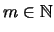 und
und 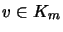
- c)
- [Bet97, p. 57] Ist K ein Matrixkegel, so gibt es ein
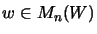 so daß für
alle
so daß für
alle
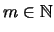 und
und 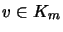
- d)
- [EW97a, Thm. 4.1] Ist K absolut matrixkonvex, so gibt es ein
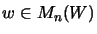 ,
so
daß für alle
,
so
daß für alle
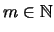 und
und 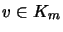
Ein Beweis des Satzes von Ruan beruht auf dem Trennungssatz für
absolut matrixkonvexe
Mengen, angewandt auf die Einheitskugel eines Operatorraums.





Next: Bipolarensätze
Up: Matrixkonvexität
Previous: Beispiele
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04
![]() eine (nicht ausgeartete) Dualität von Vektorräumen. Dadurch
sind V und W mit schwachen Topologien versehen und die Matrizenstufen mit der
zugehörigen Produkttopologie. Zu
eine (nicht ausgeartete) Dualität von Vektorräumen. Dadurch
sind V und W mit schwachen Topologien versehen und die Matrizenstufen mit der
zugehörigen Produkttopologie. Zu
![]() und
und
![]() ist
ist
![]() erklärt als die Amplifikation der Dualität:
erklärt als die Amplifikation der Dualität:
![]() bedeutet also nicht >.
bedeutet also nicht >.
![]() eine Dualität von Vektorräumen, K eine
abgeschlossene Menge von Matrizen über V, und
eine Dualität von Vektorräumen, K eine
abgeschlossene Menge von Matrizen über V, und
![]() .
.