




Next: Tensorprodukte
Up: Grundkonstruktionen
Previous: Konjugierter Hilbert-C*-Modul
- 1.
- Der komplex konjugierte Raum eines Hilbertraumes ist
mit
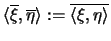 wieder ein Hilbertraum. Betrachtet man den
rechten Hilbert-
wieder ein Hilbertraum. Betrachtet man den
rechten Hilbert-
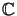 -Modul
-Modul
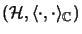 ,
so ist
sein konjugierter
Hilbert-
,
so ist
sein konjugierter
Hilbert-
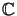 -Modul
-Modul
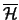 gerade der komplex konjugierte
Hilbertraum.
gerade der komplex konjugierte
Hilbertraum.
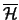 ist vollständig isometrisch zum
Zeilen-Hilbertraum
ist vollständig isometrisch zum
Zeilen-Hilbertraum
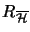 .
.
- 2.
- Für einen rechten Hilbert-C*-Modul sind der
konjugierte Spaltenraum
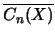 und
der Zeilenraum
und
der Zeilenraum
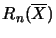 vollständig isometrisch
isomorph als linke
Hilbert-C*-Moduln über A.
Der Spaltenraum
vollständig isometrisch
isomorph als linke
Hilbert-C*-Moduln über A.
Der Spaltenraum
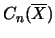 und der konjugierte Zeilenraum
und der konjugierte Zeilenraum
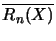 sind vollständig isometrisch isomorph als linke
Hilbert-C*-Moduln über Mn(A).
sind vollständig isometrisch isomorph als linke
Hilbert-C*-Moduln über Mn(A).
- 3.
- Ist X ein Hilbertraum
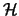 ,
so ergeben sich aus 2. mit n=1
die Spezialfälle:
,
so ergeben sich aus 2. mit n=1
die Spezialfälle:
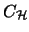 ist der Spalten-Hilbertraum .
Die vollständigen Isometrien ist in beiden Fällen durch die Identität auf
dem gemeinsamen Grundraum gegeben.
ist der Spalten-Hilbertraum .
Die vollständigen Isometrien ist in beiden Fällen durch die Identität auf
dem gemeinsamen Grundraum gegeben.
Lehrstuhl Prof. Dr. Gerd Wittstock
1999-09-04