wobei
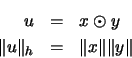
gilt. Das Infimum in der Normformel ist in diesem Fall ein Minimum [ER91, Prop. 3.5].
wobei
vollständig kontrahierend ist. Das Haagerup-Tensorprodukt hat also die Eigenschaft 2 eines Operatorraum-Tensorproduktes.
Die shuffle-Abbildung ist aber im allgemeinen keine Isometrie, wie das
folgende Beispiel zeigt:31
Da die bilineare Abbildung
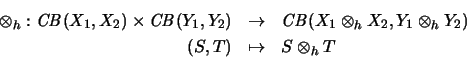
kontrahierend ist, ist sie allgemein vollständig kontrahierend.32
Sie ist aber nach 7 sogar vollständig kontrahierend.
Häufig reicht es, eine Beziehung für das Haagerup-Tensorprodukt auf der Grundstufe nachzuweisen und sie dann mit Hilfe der obigen Formel für alle Matrizenstufen zu folgern33.
Spezialfälle des Lemmas von Blecher und Paulsen sind:
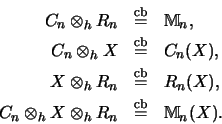
Für einen Operatorraum X gilt [Ble92b, Prop. 2.3]:
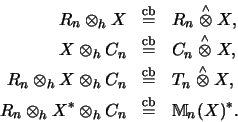
Also ist auch ihre Amplifikation,
das
tensorielle Matrixprodukt
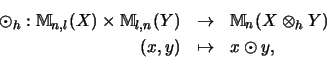
vollständig kontrahierend . Die Linearisierung des tensoriellen Matrixprodukts ergibt die vollständige Kontraktion
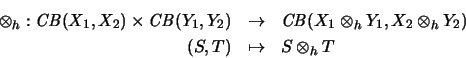
ist vollständig kontrahierend .34 35 und erzeugt eine vollständige Kontraktion
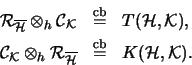
Das Beispiel zeigt auch, daß das Haagerup-Tensorprodukt nicht symmetrisch ist.