Sammelbilder würfeln – manchmal dauert’s länger als man denkt
Situation
Zur Euro 2012 wird ein Sammelalbum für 540 Sammelbilder auf den Markt gebracht. Wie üblich sind die zu kaufenden Bilder in undurchsichtigen Tüten verpackt – zu je 5 Bilder pro Päckchen.
Wie viele Päckchen muss man wohl kaufen, bis das Album voll ist?
Vergleichbare Situation – kleinere Zahlen – kostenlose Bilder
Zur EM 12 wird ein Sammelalbum für 6 Sammelbilder auf den Markt gebracht. Wie üblich sind die zu kaufenden Bilder in undurchsichtigen Tüten verpackt – zu je 2 Bilder pro Päckchen.
Wie viele Päckchen muss man wohl kaufen, bis das Album voll ist?
Um dies zu beantworten, zählen wir nun durch Würfelzahlen simulierte Bilder.
Den Inhalt eines Päckchens simulierst Du durch den Wurf zweier Würfel. Die Würfelzahlen stehen dann für zwei Bildernummern. Mache in der Tabelle jeweils einen Strich für jede gewürfelte Nummer – „bis das Album voll ist“. Zähle dann zusammen, wie viele Päckchen Du zum Erfolg brauchtest. Wiederhole dieses Vorgehen fünf Mal. Tauscht Eure Ergebnisse in der Klasse aus. Was stellt Ihr fest? Macht eine gemeinsame Statistik. Wie viele Päckchen benötigtet Ihr im Mittel?

Arbeitsblatt dazu: PDF-Datei
Zur Beantwortung kann man durch Würfelzahlen simulierte Bilder zählen. Was kann man aus dem Würfeln lernen?
Bei einer Klasse mit 25 Schülern kommen 125 Daten zusammen, deren Verteilung wie in den folgenden Diagrammen aussehen kann. Es sind dort jeweils die aufgetretenen Häufigkeiten (senkrechte Achse) der Anzahlen der benötigten Päckchen (waagerechte Achse) dargestellt. Im ersten Schaubild sieht man z.B. dass in dieser Klasse zehnmal der Fall auftrat, dass neun Päckchen benötigt wurden und es zwei Glückspilzfälle gab, in denen schon mit drei Päckchen Erfolg verzeichnet wurde, sowie einen Pechvogel, der 26 Päckchen brauchte.
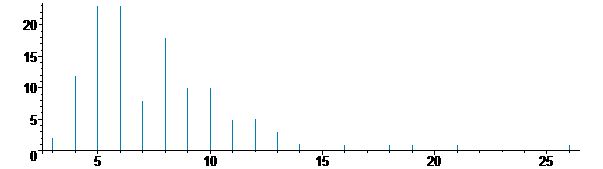
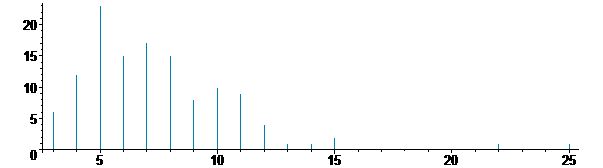
Im Mittel benötigt man 7 bis 8 Päckchen. Wegen der geringen Anzahl der Versuche, gibt es zwar schon beobachtbare Gemeinsamkeiten, aber ebenso noch beobachtbare Schwankungen. Das macht gerade den Reiz des Zufalls aus.
Wie lösen wir mit dieser Erkenntnis das Sammelbildproblem?
Wir systematisieren unsere Erfahrung. Dazu stellen wir sie zunächst übersichtlich dar. Wir nehmen die Bilder nacheinander aus dem Päckchen. Zu Beginn haben wir alle Plätze frei. Wir benötigen also nur ein Bild, um sicher einen freien Platz zu finden, d.h. um einen Treffer zu landen. Der Erwartungswert für die Anzahl der benötigten Bilder ist damit in diesem Schritt 1. Im nächsten Schritt ist nun bereits ein Platz besetzt und wir haben fünf Möglichkeiten für einen Treffer, aber auch eine für eine Niete. Im Verhältnis zur Anzahl der Treffer haben wir damit einen Nietenzuschlag von ein Fünftel, also 20% zu berücksichtigen. Das bedeutet, dass wir erwarten, im Mittel statt 1 nun 1,2 zufällige Bilder zu benötigen, um den nächsten Platz zu füllen. Jetzt sind zwei Plätze besetzt, wir haben vier Möglichkeiten für einen Treffer und zwei für eine Niete, damit einen Nietenzuschlag von 50%, also einen Erwartungswert von 1,5 … Diese Überlegung führen wir für jeden Schritt fort – „bis das Album voll ist“.
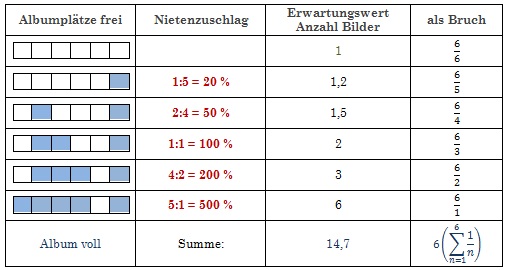
Das Addieren der Erwartungswerte für die einzelnen Schritte ergibt den Erwartungswert für die Gesamtanzahl der Bilder: 1 + 1,2 + 1,5 + 2 + 3 + 6 = 14,7. Das 14,7-te Bild wird dabei dem achten Päckchen entnommen. Zufall führt zu Abweichungen und damit faktisch zur beobachtbaren Bandbreite von Ergebnissen im Experiment.
Wie können wir mit diesem Wissen das Sammelbildproblem lösen? Wir müssen aus dem betrachteten Spezialfall das allgemeine Muster herauslesen! Dazu ist es hilfreich, die Darstellung der Zahlen zu wechseln, um mehr sehen zu können. Wir stellen, motiviert durch das Wissen, dass die Zahl 6 eine Rolle spielt, die auftretenden Erwartungswerte als Brüche dar, in denen die Zahl 6 vorkommt:
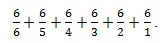
Aus dieser Summe lässt sich noch die Zahl 6 ausklammern:
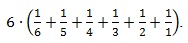
Damit kommen wir zur Einsicht, dass wir, wenn die Sammelbilderanzahl 540 beträgt, die Anzahl der im Mittel benötigten Bilder berechnen können durch 540 mal die Summe der 540 ersten sog. Stammbrüche, d.h. der Brüche mit Zähler 1:
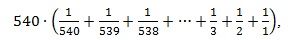
was uns 3709,643640... liefert – und 3710 Bilder, also 742 Päckchen bedeutet. Bei einem Einzelpreis von 0,60 € pro Päckchen summieren sich die Kosten insgesamt auf 445,20 €.
Diese Erläuterungen zum Ausdrucken: PDF-Datei
Kann man das auch einfacher mit dem Taschenrechner ...?
Es wäre natürlich äußerst mühsam diese längliche Rechnung selbst mit einem Taschenrechner auszuführen. Wenn man kein geeignetes Computerprogramm zur Verfügung hat, kann man sich auch mit einer passenden Näherungslösung helfen: Die Stammbruchsumme der n ersten Stammbrüche hat für große n hinreichend genau den Wert ln(n)+c, worin ln für den natürlichen Logarithmus steht und c für die Euler-Mascheroni-Konstante, die (in Taschenrechnergenauigkeit) den Wert 0,577215665 hat. Für n=540 erhalten wir so mit dem Taschenrechner
540 × ( ln(540) + 0,57721566490 ) = 3709,143795.
Und wenn es beim nächsten von Sammelbildern begleiteten Großereignis 800 unterschiedliche Bilder für Sammelwütige gäbe, dann müssten diese im Mittel 800 × ( ln(800) + 0,57721566490 ) = 5809 Bilder in 1162 Päckchen kaufen.
742 - mal weniger, mal mehr
Im Mittel erwartet man also 742 notwendige Päckchen bei 540 unterschiedlichen Sammelbildern. Aber Zufall führt bekanntlich zu Abweichungen. Die folgende Abbildung zeigt das Ergebnis einer Computersimulation von 5000 Sammlern, die ihr Album gefüllt haben oder bei 1200 Päckchen frustriert aufgegeben haben:
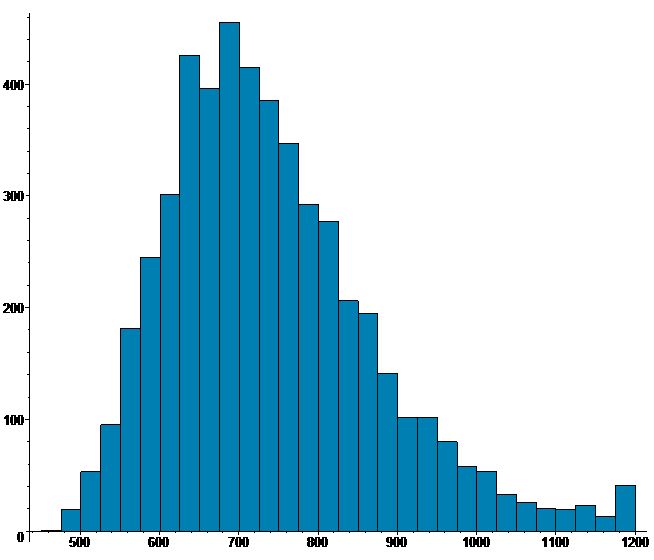
Wir können aus dem Diagramm herauslesen, dass es unter den 5000 Sammlern nur ca. 20 - also weniger als ein Halbes Prozent - Glückspilze gab, die ihr Album mit dem Inhalt von weniger als 500 Päckchen, also immerhin schon 2500 gekauften Bildern füllen konnten; knapp die Hälfte der Sammler liegt im Bereich von 650-800 Päckchen um den Erwartungswert 742 Päckchen; ca. jeder zwanzigste Sammler benötigte mehr als 1000 Päckchen und ein paar Dutzend haben das Album nach 1200 Päckchen immer noch nicht voll.
Autor: Anselm Lambert
