Dr. Roland Friedrich
Dr. Tobias Mai
Complex Analysis II
(Funktionentheorie II)
Introduction to Geometric Function Theory
and Schramm-Loewner Evolution
(Winter Semester 2017/2018)
News
- On January 30, at 4:15 pm (i.e., instead of the tutorial),
there will be an additional lecture.
- Assignment 6 (for the tutorial on January 23)
- Assignment 5 (for the tutorial on January 16)
Lecture
Tuesday, 12 -- 14, Seminar Room 10, Building E2 4|
In geometric function theory, holomorphic functions are regarded as mappings between subsets of the complex plane and one aims at understanding the rich interplay between their geometric and analytic properties. Of interest are especially conformal maps, namely holomorphic functions that are additionally injective. Among the numerous powerful tools that were developed for this purpose is the so-called Loewner evolution. It can be seen as a dynamical process 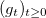 on the set of conformal maps, which describes the evolution of some curve in a fixed simply connected domain.
On the complex upper half plane on the set of conformal maps, which describes the evolution of some curve in a fixed simply connected domain.
On the complex upper half plane  , it is determined by the chordal Loewner equation , it is determined by the chordal Loewner equation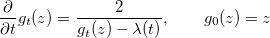 with respect to some driving function 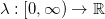 . .In 2000, Oded Schramm added a stochastic component to that theory by considering driving functions 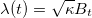 for for 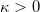 and with and with
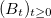 being the one-dimensional Brownian motion. This results in a kind of Brownian motion on the space of conformal maps, called the stochastic Loewner evolution being the one-dimensional Brownian motion. This results in a kind of Brownian motion on the space of conformal maps, called the stochastic Loewner evolution 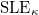 , i.e., a family , i.e., a family 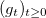 of random conformal maps associated to some random curve in of random conformal maps associated to some random curve in 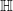 . .The character of 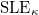 strongly depends on strongly depends on 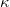 . Their relevance lies in the fact that they are (conjectured to be) the scaling limit of various discrete random processes appearing in mathematics and physics, such as the loop-erased random walk and percolation. . Their relevance lies in the fact that they are (conjectured to be) the scaling limit of various discrete random processes appearing in mathematics and physics, such as the loop-erased random walk and percolation.With Wendelin Werner (2006) and Stanislav Smirnov (2010), two mathematicians have been awarded the Fields medal for their contributions to this fascinating field. In this lecture, which is formally a continuation of the lecture Funktionentheorie, we give an introduction to the basics of both geometric function theory and stochastic Loewner evolution. We will also provide the needed facts from probability theory and stochastic calculus. Participants are supposed to have some prior knowledge on basic measure theory and complex analysis (such as Analysis III and Funktionentheorie), but no prerequisites on probability theory are assumed. |
Lecture announcement
KVV Winter term 2017/2018
For further information, please contact Tobias Mai.
Lecture notes
Lecture notes, October 17Lecture notes, October 24
Lecture notes, November 7
Lecture notes, November 14
Lecture notes, November 21
Lecture notes, November 28
Lecture notes, December 5
Lecture notes, December 12
Tutorials
The tutorials (problem sessions) take place every second week onTuesday, 16 -- 18, in Seminar Room 10, Building E2 4.
The next meeting is on January 23.
Assignment 1A (for the tutorial on November 7) Solution Assignment 1A
Assignment 1B (for the tutorial on November 7) Solution Assignment 1B
Assignment 2A (for the tutorial on November 21) Solution Assignment 2A
Assignment 2B (for the tutorial on November 21) Solution Assignment 2B
Assignment 3A (for the tutorial on December 5) Solution Assignment 3A
Assignment 3B (for the tutorial on December 5) Solution Assignment 3B
Assignment 4A (for the tutorial on December 12) Solution Assignment 4A
Assignment 5 (for the tutorial on January 16)
Assignment 6 (for the tutorial on January 23)
You do not have to hand in written solutions. We will discuss the problems in
the tutorials, but you should be prepared then to present your solution.
References
- A. Baernstein: The Bieberbach conjecture: proceedings of the symposium
on the occasion of the proof, AMS - J. B. Conway: Functions of one complex variable 1/2, Springer
- S. Gong: The Bieberbach conjecture, AMS
- G. F. Lawler: Conformally invariant processes in the plane, AMS
- G. F. Lawler: Intersections of random walks, Birkhäuser
- G. F. Lawler, V. Limic: Random walk: a modern introduction, Cambridge University Press
- C. Pommerenke: Boundary behaviour of conformal maps, Springer
- T. Ransford: Potential theory in the complex plane, Cambridge University Press
- R. Remmert, G. Schumacher: Funktionentheorie 1/2, Springer
- W. Rudin: Real and complex analysis, McGraw-Hill
provided by the Campusbibliothek für Informatik und Mathematik.
updated: 23 January 2018 Tobias Mai

